动机
Knowledge graph通常是采用三元组表征实体之间的关系,由于构建成本和覆盖面影响,一个重要问题是如何基于观察到的事实进行推理预测缺少的事实;- 一种方法是基于规则的符号逻辑方法,如
Markov Logic Network结合first-order logic和概率图模型,利用域知识来处理不确定性,但由于复杂的图结构及规则的限制,导致推理通常很困难;
- 另一种方法是知识图嵌入方法,
knowledge graph embedding能有效地学习有用的entity embedding和relation embedding进行推理,但不能利用逻辑规则。
贡献
- 提出概率逻辑神经网络
pLogicNet,该方法同时结合MLN和知识图嵌入方法的优点,既能够利用一阶逻辑规则并处理其不确定性,也能够以有效的方式训练和推断缺失的三元组;
- 该方法利用一阶马尔可夫逻辑网络定义了所有可能三元组的联合分布,其将每个逻辑规则与权值关联起来,并用变分
EM算法进行有效优化。在E步中,使用知识图嵌入模型推断缺失的三元组,在M步中,根据观察到的三元组和预测的三元组更新逻辑规则的权值。
相关概念
问题定义
Knowledge graph是关系事实的集合,每个事实表示为一个三元组,知识图推理的问题定义如下:形式上,给定一个knowledge graph,其中是实体集合,是关系集合,是一组观测到的,其目标是通过对观察到的三元组进行推理来推断缺失的三元组。即对于每个三元组,均与一个二元指示函数关联,表示为真,否则;给定一些真实的事实,目标是预测剩余隐藏的三元组的标签。
Markov Logic Network
MLN设计一个马尔可夫网络来定义观测三元组和隐藏三元组的联合分布,其中势能函数由一阶逻辑定义,一些常见的编码域知识的逻辑规则包含:
Composition Rules
组合规则,即与有的关系,与有的关系,则与有的关系,其中是和的组合:
Inverse Rules
反向规则,即与有的关系,则与有的关系:
Symmetric Rules
对称规则,即与有的关系,则与也有的关系:
Subrelation Rules
子关系规则,即与有的关系,则与也有的关系:
对于每个逻辑规则,可以通过knowledge graph中的实体关系在逻辑规则中的实例化来获得可能的groundings,比如Subrelation Rules,,但这种规则可能不成立,故对每个逻辑规则引入权重来评估不确定性,三元组的联合分布定义为:
其中,为逻辑规则基于和的值真实存在的groundings数量。通过上述式子,预测缺失的三元组即为推断后验分布,通常使用近似推断,如MCMC和loopy belief propagation。
Knowledge Graph Embedding
知识图嵌入方法首先利用观察到的事实学习实体embeddings和关系embeddings,然后利用所学的实体embeddings和关系embeddings预测缺失的事实。形式上,每个实体和关系通过embedding和相关联,三元组的联合分布定义为:
其中,是伯努利分布,计算三元组为真的概率,是实体和关系embeddings的评分函数,本文采用TransE方法中的,其中为sigmoid函数,为固定的bias。为了学习实体和关系embeddings,通常将观察三元组记作正样本,将隐藏三元组记作负样本,通过最大化对数似然函数,采用随机梯度下降进行优化。
pLogicNet
pLogicNet结合基于规则的逻辑网络和知识图嵌入方法,为了利用一阶逻辑规则所提供的域知识,pLogicNet使用马尔科夫逻辑网络计算所有三元组的联合分布。通过变分EM算法进行训练,E步采用知识图嵌入模型推断缺失三元组,可以有效地将逻辑规则所保存的知识蒸馏为学习的embeddings,M步根据观察到的三元组和知识图嵌入模型推断的缺失三元组对逻辑规则的权值进行更新,为权重的学习提供额外监督信息。
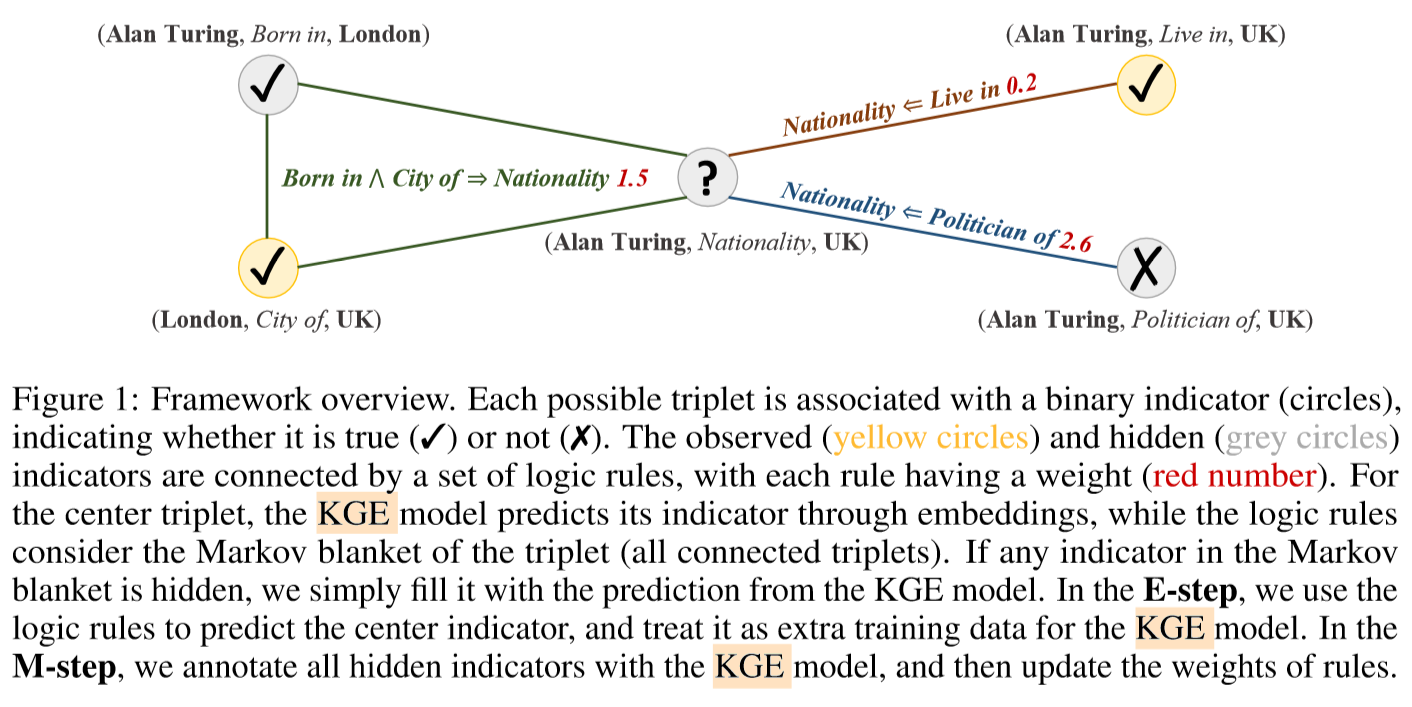
如上图所示,每个三元组关联一个二元指示器(圆圈,或),观测三元组(黄色圆圈)和隐藏三元组(灰色圆圈)通过一组逻辑规则相连,每个规则有一个权重(红色数字)。对于中心的三元组,通过knowledge graph embedding预测其指示器,同时逻辑规则使用所有Markov blanket相连三元组。在E步,使用逻辑规则预测中心指示器,并将其作为训练knowledge graph embedding模型的额外训练数据,在M步,使用knowledge graph embedding标注所有隐藏指示器,然后更新逻辑规则的权重。
Variational EM
给定一个一阶逻辑规则集合,使用MLN建模观测三元组和隐藏三元组的联合分布:
该模型通过最大化观测指标器变量的对数似然来训练,近似为优化对数似然函数的变分下界:
其中为隐藏变量的变分分布,当等于真实后验分布时方程成立。变分E步称为推断过程,固定并更新,使得最小化和的KL距离;变分M步称为学习过程,固定并更新,使得最大化所有三元组的对数似然函数。
E-step
目的:推断隐藏三元组的后验概率
根据平均场理论使用近似真实后验分布,并将每个三元组对应的参数化为KGE:
通过最小化和的KL距离,即:
其中,是的Markov blanket,包含在逻辑规则下一起出现的三元组。参考Stochastic variational inference,通过采样去估计期望,具体而言,对于每个,如果它被观测,则,否则,则目标简化为:
直观上,对于每个隐藏三元组,KGE通过实体embedding和关系embedding预测,即,同时逻辑规则则预测与相连的三元组,即,如果任何与相连的都是未被观测的,则采样填充。
最终优化目标由两部分构成:
即对于,通过逻辑规则计算隐藏三元组(当大于某个阈值时则为正样本,否则为负样本),然后通过最大似然估计去训练KGE;对于,即根据观测三元组的标签,通过最大似然估计去训练KGE。通过上述损失函数,由逻辑规则捕获的知识可以有效地蒸馏到知识图嵌入模型中。
M-step
固定并通过最大化对数似然估计函数去更新逻辑规则权值,简化伪似然估计:
其中第二个式子由MLN方程中的独立性导出,对每个,假设和通过规则集合相连,对于每个规则,对求导:
如果是观测三元组,则,否则,是从采样的样本,如果是观测三元组,则,否则。
即对于观测三元组,希望逻辑规则结果为真实标签,对于隐藏三元组,希望逻辑规则结果接近KGE的结果。通过上述损失函数,知识图嵌入模型实质上为学习逻辑规则权值提供了额外的监督。
优化与预测
优化:
未观测三元组数量过多,在训练时只将一部分未观测加入隐藏三元组,即通过如下方式:即通过观测三元组premise,且有事实:premise$$\Rightarrow$$hypothesis的hypothesis未观测三元组。
预测:
虽然训练时尽量鼓励与一致,但由于使用信息的不同,仍可能给出不同的预测,故使用:
又对于,KGE很容易进行推断,而逻辑规则很难预测,故简单的令。
部分实验结果
评测方法:
对于每个三元组,对头/尾实体进行mask,然后预测被mask的实体。
评测指标:
MR:平均排名,即对于返回的结果按照分数高低排名,所以越小越好;
MRR:平均倒数排名,即对于返回的结果按照分数高低排名,得分为它的排名,所以越大越好;
H@K:即按分数排名,然后去看每个三元组的正确答案是否排在预测序列的前个,计算其占比,所以越大越好。
比较不同的知识图推理方法:
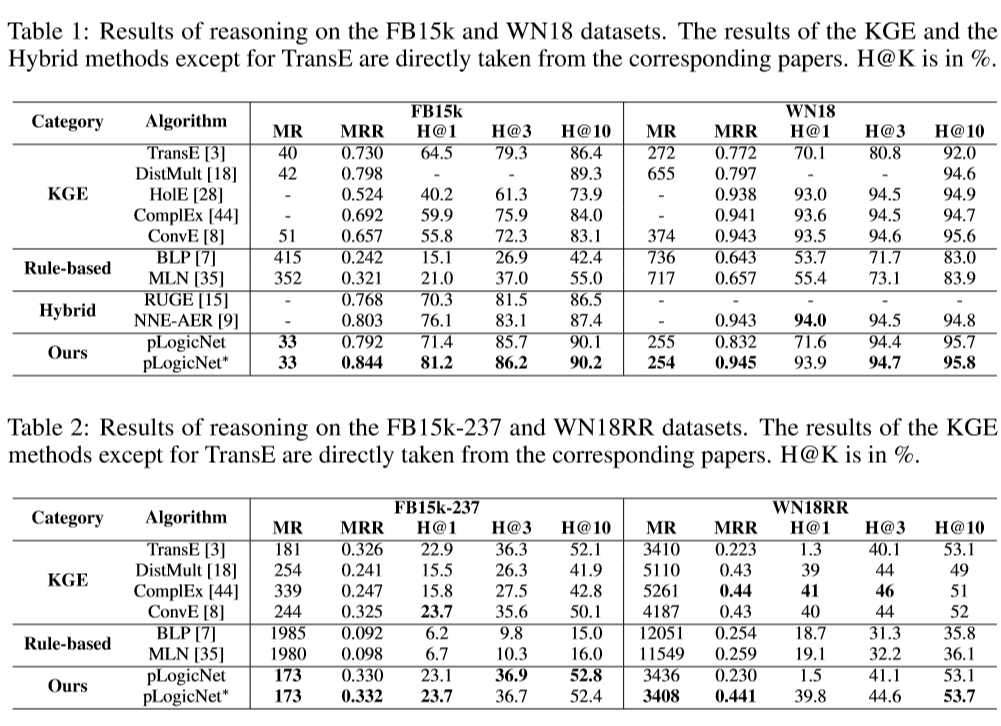
其中pLogicNet为仅使用进行推断,pLogicNet*表示通过和联合进行推断。
比较不同的逻辑规则:
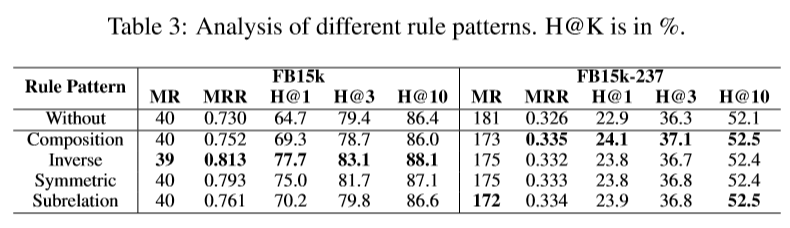
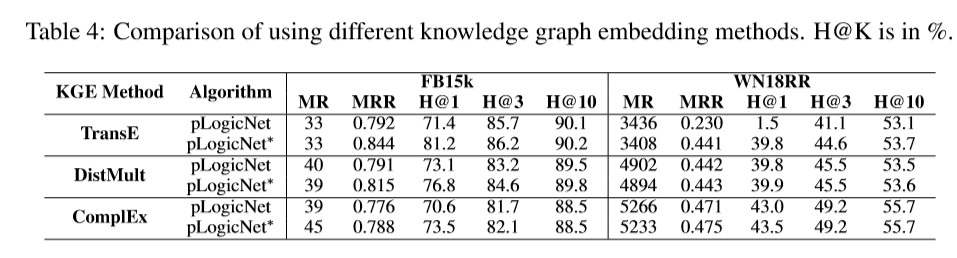
比较不同的知识图嵌入方法: