动机
基于AR的语言模型通过autoregressive model将估计文本语料库的概率分布,将似然因式分解为前向乘积或后向乘积,并对每个条件分布进行建模。其通常仅通过单向上下文进行预训练,而下游任务通常需要双向的上下文信息;
基于AE的语言模型通过denoising autoencoder从损坏的输入中重建原始数据,由于不执行显式的密度估计,因此可利用双向上下文进行重建,并消除了预训练和下游任务的双向信息差异。但其引入了mask造成预训练和微调时输入的差异,且假定对于给定的unmasked tokens,每个预测的tokens彼此独立,该假设过度简化了。
贡献
提出一种通用的自回归模型XLNET,该方法同时利用了AR和AE语言模型的优点,一方面利用双向上下文信息,另一方面不会造成预训练和微调差异,且避免了BERT关于mask的独立性假设;
XLNET对Transformer-XL重参数化,将其segment recurrence mechanism和relative encoding scheme集成到预训练中;XLNET在多个任务上实现了最先进的效果,包括语言理解、阅读理解、文本分类、文档排名等任务。
XLNET背景 给定文本序列
\mathbf{x}=[x_1,…,x_T]
AR语言模型通过将最大化似然估计前向自回归分解:
\max _{\theta} \log p_{\theta}(\mathbf{x})=\sum_{t=1}^{T} \log p_{\theta}\left(x_{t} \mid \mathbf{x}_{<t}\right)=\sum_{t=1}^{T} \log \frac{\exp \left(h_{\theta}\left(\mathbf{x}_{1: t-1}\right)^{\top} e\left(x_{t}\right)\right)}{\sum_{x^{\prime}} \exp \left(h_{\theta}\left(\mathbf{x}_{1: t-1}\right)^{\top} e\left(x^{\prime}\right)\right)}
其中,
h_{\theta}\left(\mathbf{x}_{1: t-1}\right)
e(x)
x
embedding。BERT则基于denoising autoencoder,首先将
\mathbf{x}
mask构造得到
\hat{\mathbf{x}}
mask的tokens为
\overline{\mathbf{x}}
\hat{\mathbf{x}}
\overline{\mathbf{x}}
\max _{\theta} \log p_{\theta}(\overline{\mathbf{x}} \mid \hat{\mathbf{x}}) \approx \sum_{t=1}^{T} m_{t} \log p_{\theta}\left(x_{t} \mid \hat{\mathbf{x}}\right)=\sum_{t=1}^{T} m_{t} \log \frac{\exp \left(H_{\theta}(\hat{\mathbf{x}})_{t}^{\top} e\left(x_{t}\right)\right)}{\sum_{x^{\prime}} \exp \left(H_{\theta}(\hat{\mathbf{x}})_{t}^{\top} e\left(x^{\prime}\right)\right)}
其中,
m_t=1
x_t
mask,
H_{\theta}
Transformer将长度为
T
\mathbf{x}
H_{\theta}(\mathbf{x}) = [H_{\theta}(\mathbf{x})_1,…,H_{\theta}(\mathbf{x})_T]
AE和AR的预训练语言模型主要差异如下:
Independence Assumption:BERT基于所有被mask的token独立重构的假设,对联合条件概率
p_{\theta}(\overline{\mathbf{x}} \mid \hat{\mathbf{x}})
AR则使用普遍适用的乘积规则对
p_{\theta}(\mathbf{x})
Input noise:BERT输入包含[MASK],在下游任务中未出现会导致预训练和微调的差异,原文以一定概率使用原始token替换[MASK]并不能解决该问题,而AR不依赖任何输入损坏,则不会出现该问题;Context dependency:AR中
h_{\theta}\left(\mathbf{x}_{1: t-1}\right)
BERT中
H_{\theta}(\mathbf{x})_t
目标函数
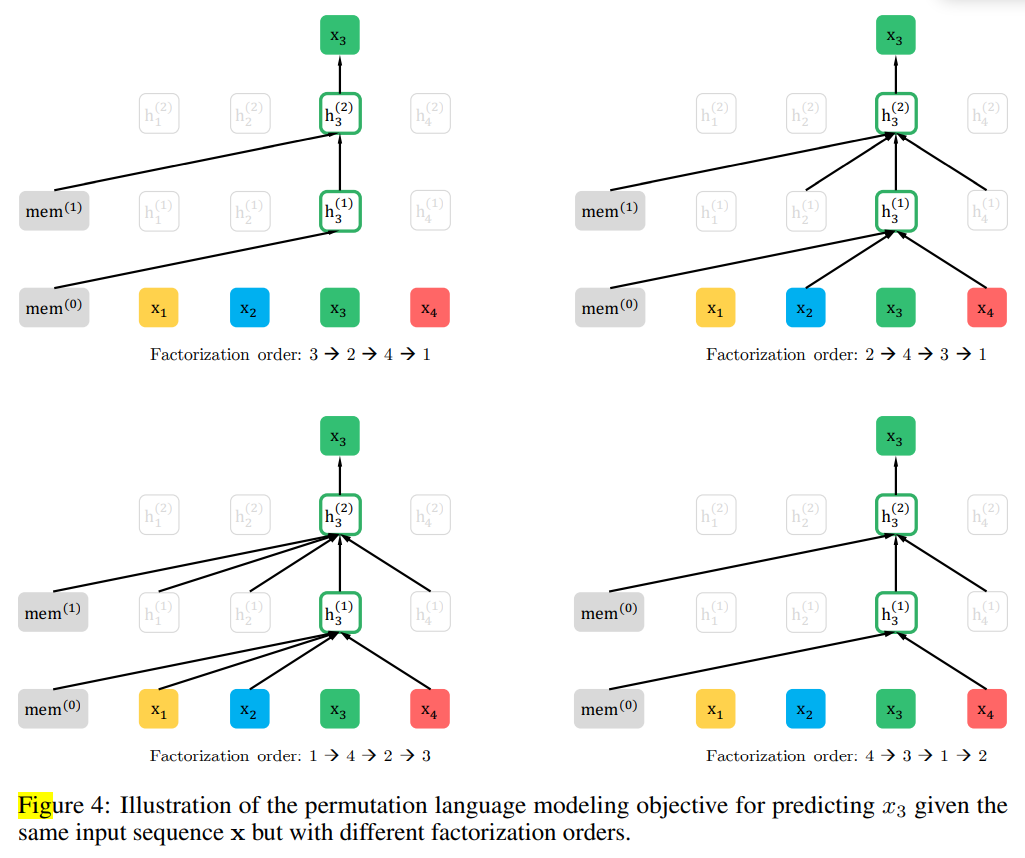
使用Permutation Language Modeling综合AR和BERT方法的优点
借鉴orderless NADE的方法,提出排列语言建模(Permutation Language Modeling)的目标函数。对于长度为
T
\mathbf{x}
T!
对于长度为
T
[1,…,T]
\mathcal{Z}_T
\max _{\theta} \mathbb{E}_{\mathbf{z} \sim \mathcal{Z}_{T}}\left[\sum_{t=1}^{T} \log p_{\theta}\left(x_{z_{t}} \mid \mathbf{x}_{\mathbf{z}_{<t}}\right)\right]
其中,
z_t
\mathbf{z}<t
\mathbf{z} \in \mathcal{Z}_T
t
t-1
\mathbf{x}
\mathbf{z}
p_{\theta}(\mathbf{x})
x_t
x_i \ne x_t
AR,自然避免了独立性假设和预训练微调差异的影响。
本文在实现时,保持原始的序列排序及对应于原始序列的位置编码,通过Transformer中的attention mask实现因式分解的排列顺序,这样不会改变输入方式,从而不会影响微调时的输入。
网络结构
基于Target-Aware表征的Two-Stream Self-Attention
Target-Aware Representation虽然permutation language modeling能满足目前的目标,但简单地使用标准的Transformer并不一定有效。假设使用标准softmax参数化下一个token的分布:
p_{\theta}(X_{z_t}=x\mid \mathbf{x}_{\mathbf{z} < t})=\frac{\exp \left(e(x)^{\top} h_{\theta}\left(\mathbf{x}_{\mathbf{z}<t}\right)\right)}{\sum_{x^{\prime}} \exp \left(e\left(x^{\prime}\right)^{\top} h_{\theta}\left(\mathbf{x}_{\mathbf{z}<t}\right)\right)}
其中,
h_{\theta}(\mathbf{x}_{\mathbf{z}<t})
\mathbf{x}_{\mathbf{z}<t}
\mathbf{x}_{\mathbf{z}<t}
mask的输入经过transformer得到。
h_{\theta}(\mathbf{x}_{\mathbf{z}<t})
token的位置
z_t
transformer都预测得到相同的分布,由此无法学习到有效的表征。
即假设两个排列
\mathbf{z}^{(1)}
\mathbf{z}^{(2)}
\mathbf{z}^{(1)}_{<t} = \mathbf{z}^{(2)}_{<t}
z^{(1)}_{t}=i\ne j= z^{(2)}_{t}
p_{\theta}(X_{i}=x\mid \mathbf{x}_{\mathbf{z}^{(1)} < t})=p_{\theta}(X_{j}=x\mid \mathbf{x}_{\mathbf{z}^{(2)} < t})=\frac{\exp \left(e(x)^{\top} h_{\theta}\left(\mathbf{x}_{\mathbf{z}<t}\right)\right)}{\sum_{x^{\prime}} \exp \left(e\left(x^{\prime}\right)^{\top} h_{\theta}\left(\mathbf{x}_{\mathbf{z}<t}\right)\right)}
即对于不同位置
i
j
token的分布,使其能感知目标位置:
p_{\theta}\left(X_{z_{t}}=x \mid \mathbf{x}_{z_{<t}}\right)=\frac{\exp \left(e(x)^{\top} g_{\theta}\left(\mathbf{x}_{\mathbf{z}_{<t}}, z_{t}\right)\right)}{\sum_{x^{\prime}} \exp \left(e\left(x^{\prime}\right)^{\top} g_{\theta}\left(\mathbf{x}_{\mathbf{z}_{<t}}, z_{t}\right)\right)}
其中,
g_{\theta}\left(\mathbf{x}_{\mathbf{z}_{<t}}, z_{t}\right)
z_t
Two-Stream Self-Attention虽然,target-aware representation能消除目标预测的模糊性,但如何构建$g_{\theta}\left(\mathbf{x}_{\mathbf{z}_{t
,
,
content
x_{z_t}
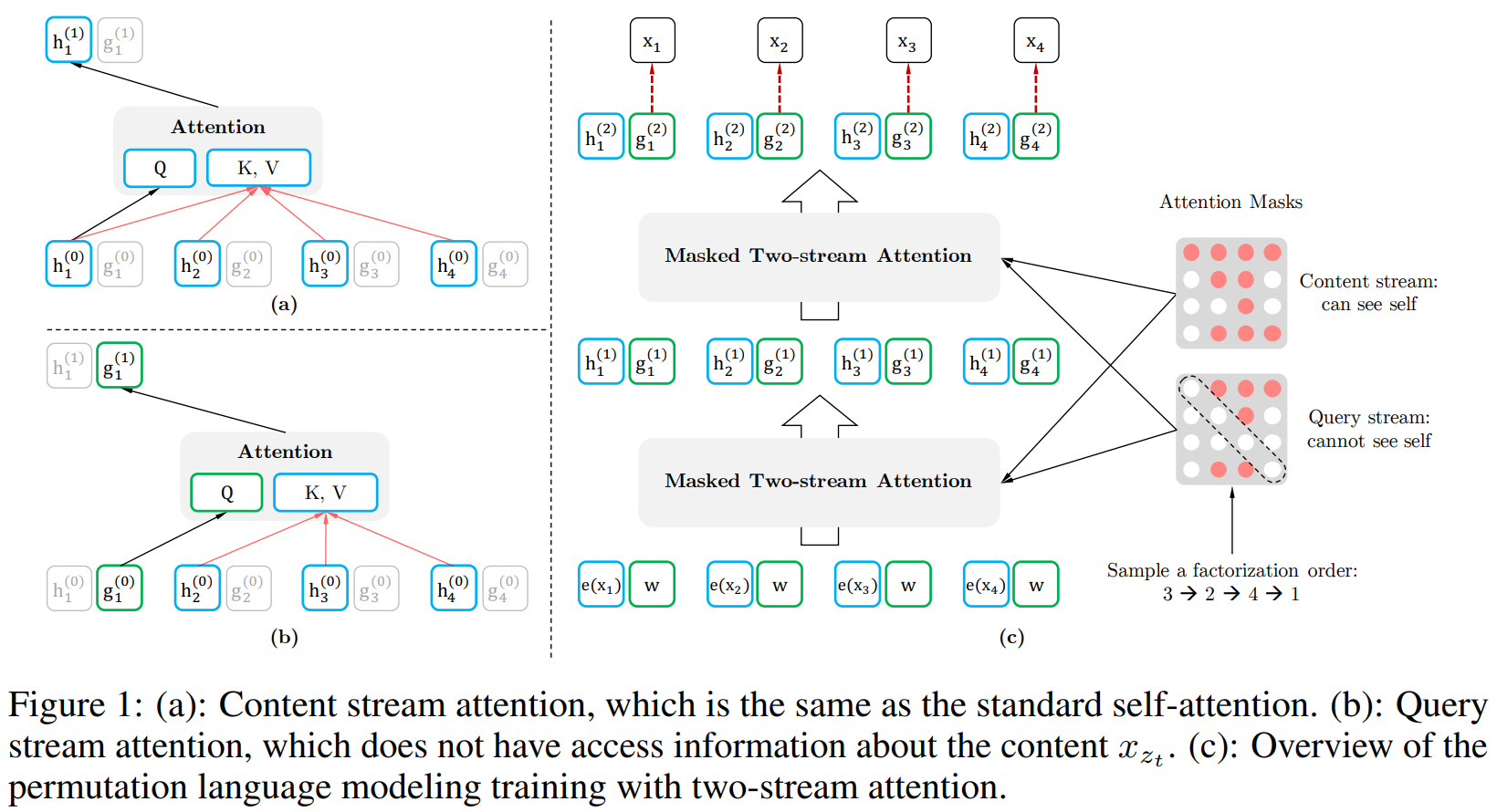
为了解决此矛盾,本文使用两组隐表征(即每个词具有两个属性,预测自己时不需要自己的内容信息,预测其他词时作为context需要内容信息):
content表征
h_{\theta}(\mathbf{x}_{\mathbf{z}_{\le t}})
h_{z_t}
Transformer,由context和
x_{z_t}
query表征
g_{\theta}\left(\mathbf{x}_{\mathbf{z}_{<t}}, z_{t}\right)
g_{z_t}
context信息
\mathbf{x}_{\mathbf{z}_{<t}}
z_t
content
x_{z_t}
实际计算时,第一层网络的query stream被初始化为可训练的向量
g_i^{(0)} = w
content stream被设置为对应的word embedding
h_i^{(0)} = e(x_i)
m
two stream表征共享参数进行更新:
\begin{aligned}
&g_{z_{t}}^{(m)} \leftarrow \operatorname{Attention}\left(\mathrm{Q}=g_{z_{t}}^{(m-1)}, \mathrm{KV}=\mathbf{h}_{\mathrm{z}_{<t}}^{(m-1)} ; \theta\right) \\
&h_{z_{t}}^{(m)} \leftarrow \operatorname{Attention}\left(\mathrm{Q}=h_{z_{t}}^{(m-1)}, \mathrm{KV}=\mathbf{h}_{\mathrm{z}_{\leq t}}^{(m-1)} ; \theta\right)
\end{aligned}
如图所示,query stream使用
z_t
x_{z_t}
content stream同时使用
z_t
x_{z_t}
query表征
g_{z_t}^{(M)}
content表征与传统self-attention一致,在微调阶段,舍弃掉query stream而只使用content stream,故微调阶段与BERT一致。
Partial Prediction全排列导致实验收敛缓慢,故仅预测因式分解顺序中最后的部分tokens,将
\mathbf{z}
c
\mathbf{z}_{\le c}
\mathbf{z}_{> c}
\max _{\theta} \mathbb{E}_{\mathbf{z} \sim \mathcal{Z}_{T}}\left[\log p_{\theta}\left(\mathbf{x}_{\mathbf{z}_{>c}} \mid \mathbf{x}_{\mathbf{z}_{\leq c}}\right)\right]=\mathbb{E}_{\mathbf{z} \sim \mathcal{Z}_{T}}\left[\sum_{t=c+1}^{|\mathbf{z}|} \log p_{\theta}\left(x_{z_{t}} \mid \mathbf{x}_{\mathbf{z}_{<t}}\right)\right]
选用
\mathbf{z}_{>c}
\mathbf{z}
context。对于非目标的tokens,则不需要计算query表征,可以加速和减少运行内存。
因为本文使用AR框架的目标函数,故可引入Transformer-XL作为预训练框架,并集成相对位置编码(relative positional encoding scheme) 和片段循环机制(segment recurrence mechanism)。
segment recurrence mechanism
主要用于解决超长序列的依赖问题,对于特别长的序列会导致丢失一些信息,Transformer-XL即将序列分割为多个segment,计算后面的segment时依赖前一segment的隐特征。
假设长序列的两个segment
\tilde{\mathbf{x}}=\mathbf{s}_{1:T}
\mathbf{x}=\mathbf{s}_{T+1:2T}
\tilde{\mathbf{z}}
\mathbf{z}
[1,…,T]
[T+1,…,2T]
\tilde{\mathbf{z}}
segment,缓存层
m
content表征
\tilde{\mathbf{h}}^{(m)}
segment,注意力更新变为:
h_{z_{t}}^{(m)} \leftarrow \operatorname{Attention}\left(\mathrm{Q}=h_{z_{t}}^{(m-1)}, \mathrm{KV}=\left[\tilde{\mathbf{h}}^{(m-1)}, \mathbf{h}_{\mathbf{z}_{\leq t}}^{(m-1)}\right] ; \theta\right)
其中,
[\cdot,\cdot]
concate,因为位置编码仅取决于原始序列中的实际位置,则获得
\tilde{\mathbf{h}}^{(m)}
\tilde{\mathbf{z}}
segment时可以缓存和使用之前segment的隐状态。
relative segment encodings
BERT在每个位置的word embedding使用绝对segment编码,与当前内容在原始序列的相对位置没有关系,导致了位置信息的损失。使用relative segment encodings引入inductive bias提升泛化,且对于两个以上输入segment的任务可以进行微调。
给定序列中的一对位置
i
j
i
j
segment,则定义segment encoding
\mathbf{s}_{ij}=\mathbf{s}_{+}
\mathbf{s}_{ij}=\mathbf{s}_{-}
\mathbf{s}_{+}
\mathbf{s}_{-}
attention head学习的模型参数。即只考虑两个位置是否来自同一segment,而不是是否来自特定的segment。引入相对编码后,计算注意力的权重
a_{ij} = (\mathbf{q}_i + \mathbf{b})^{\top}\mathbf{s}_{ij}
\mathbf{q}_i
attention的query向量,
\mathbf{b}
head的偏置向量,最后将
a_{ij}
\text{softmax}(\frac{Q\cdot K}{d}V)
与BERT的比较 预训练阶段与BERT类似,输入形式为
[A, SEP, B, SEP, CLS]
NSP任务,只使用了来自同一上下文的序列。
通过比较目标函数,BERT和XLNET均使用部分预测。但BERT的独立性假设,使得BERT无法建模预测目标之间的依赖关系。例如输入序列为[New, York, is, a, city],假设BERT和XLNET均选择[New, York]为预测目标,以及XLNET的因式分解顺序为[is, a, city, New, York],均最大化目标函数
\log p(\text{New York}\mid \text{is a city})
\begin{aligned}
\mathcal{J}_{\mathrm{BERT}}=\log p(\text{New} \mid \text{is a city})+\log p(\text{York} \mid \text{is a city}), \\
\mathcal{J}_{\mathrm{XLNet}}=\log p(\text{New} \mid \text {is a city})+\log p(\text{York} \mid \text{New, is a city}) .
\end{aligned}
即XLNET能捕获[New York]的依赖对信息,虽然BERT也能学习一些依赖对,但XLNET在相同目标情况下能学习更多的依赖对,包含更密集的训练信息。更一般地,给定序列
\mathbf{x}=[x_1,…,x_T]
target-context对
\mathcal{I}=\{(x,\mathcal{U})\}
\mathcal{U}
x
tokens
\mathcal{T}
tokens
\mathcal{N}=x \text{\\}\mathcal{T}
BERT和XLNET均最大化
\log p(\mathcal{T}\mid \mathcal{N})
\mathcal{J}_{\mathrm{BERT}}=\sum_{x \in \mathcal{T}} \log p(x \mid \mathcal{N}) ; \quad \mathcal{J}_{\mathrm{XLNet}}=\sum_{x \in \mathcal{T}} \log p\left(x \mid \mathcal{N} \cup \mathcal{T}_{<x}\right)
其中,
\mathcal{T}_{<x}
\mathcal{T}
x
tokens。如果
\mathcal{U} \subseteq \mathcal{N} \cup \mathcal{T}_{<x}
\mathcal{U} \cap \mathcal{T}_{<x}\ne \emptyset
XLNET能覆盖更多的依赖项,则XLNET能获得更多有效的训练信息,使得获得更好的效果。
训练过程 数据集: BooksCorpus,English Wikipedia,Giga5,ClueWeb 2012-B和Common Crawl
分词: SentencePiece
训练细节:
batchsize为
8192
token长度为
512
Adam优化器和线性学习率衰减。设置partial prediction的超参数
K=\frac{|\mathbf{z}|}{|\mathbf{z}|-c}=6
BERT大致相同。本文使用span-based prediction,即先采样
L \in [1,…,5]
L
tokens的span作为预测目标,上下文则包含
KL
tokens。
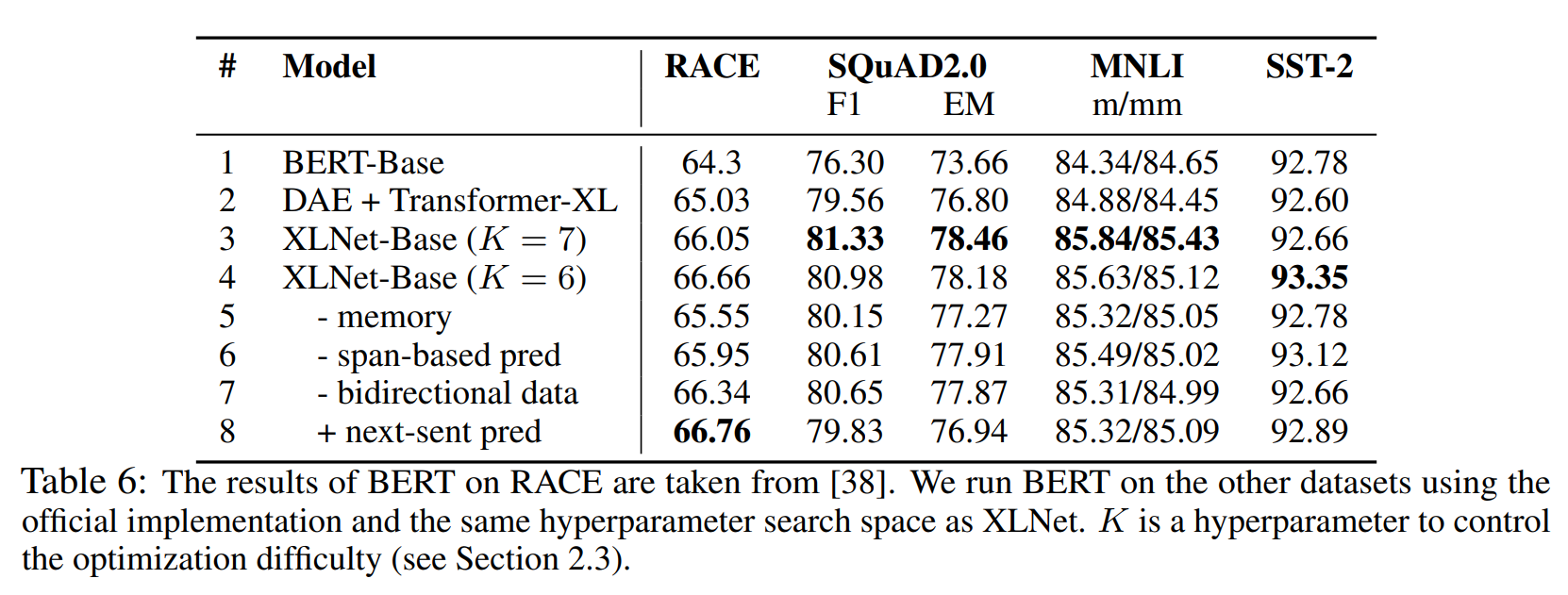
部分实验结果 Ablation Study:
如图所示:
permutation language modeling优于denoising auto-encoding;Transformer-XL作为backbone的有效性;memory(即segment recurrence mechanism)对长文本任务影响较大;span-based prediction和bidirectional data也起着重要作用;next sentence prediction无明显影响;