论文综述-contrastive learning-对比损失

2021-11-4 update Contrastive loss, Triplet loss, NCE, InfoNCE

Contrastive loss

论文文献：Dimensionality Reduction by Learning an Invariant Mapping

参考博客：文献阅读 - Dimensionality Reduction by Learning an Invariant Mapping

文章提出一种称为DrLIM的降维方法，用于学习全局一致的非线性函数，该函数将高维数据均匀映射到低维输出流形。在训练时，仅依赖于领域关系，而不需要输入空间中的距离度量，且该方法可以学习到对输入的某些变换不变的映射。

目标：学习一个映射函数，使得低维输出流形上的距离度量类似于高维输入空间的近邻关系。

假设输入样本集合为，定义第组样本的损失函数为：

其中，为模型权重，为标识符，表示样本之间是否相似(表示相似、表示不相似)，为隐空间的欧式距离(定义为)。和分别为正样本对和负样本对情况下的损失函数。

所以，整体的损失为：

对于正负样本对情况下的损失函数，要求满足下图的趋势(为红色，为蓝色)

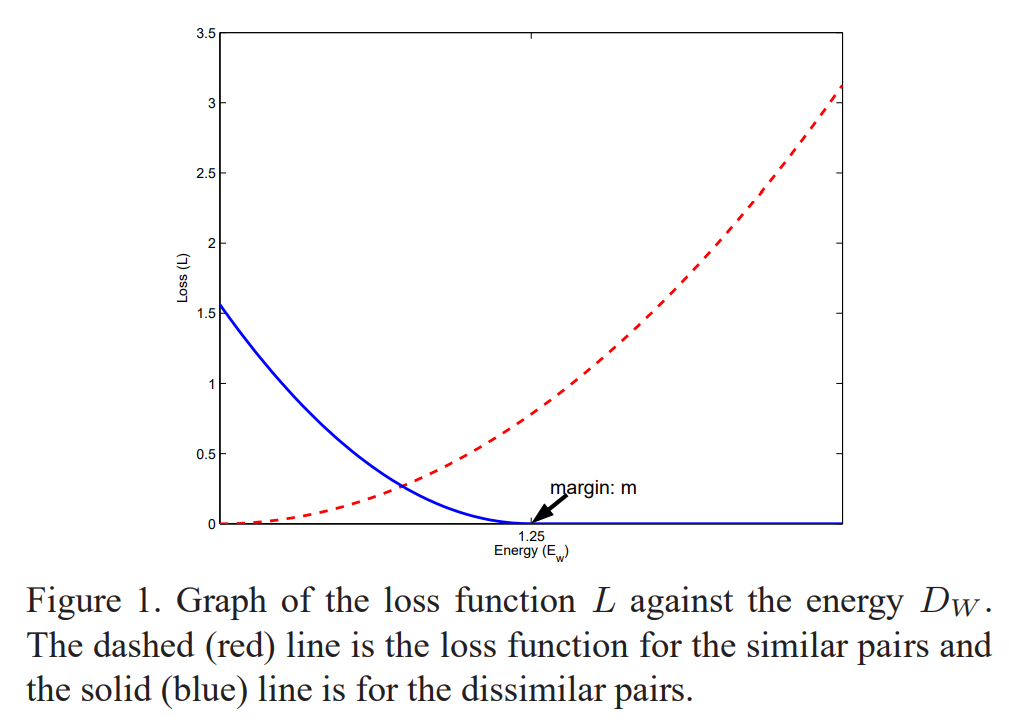
文章从弹性势能出发，进行讨论。定义弹簧模型为

正样本对

当与锚点为正样本时，两者之间会逐渐靠近。

假设弹簧为拉力弹簧(attract-only)，静止长度，即任意正位移均导致弹簧产生拉力，从而使得正样本无限拉近，从而完成聚类。

将锚点设为零势能点，则：

则由此得到：
负样本对

当与锚点为负样本时，两者之间会逐渐远离。

假设弹簧为斥力弹簧(m-repulse-only)，静止长度，当位移小于时，负样本间相互排斥，从而完成边界划分。

将锚点设为零势能点，则：

则由此得到：

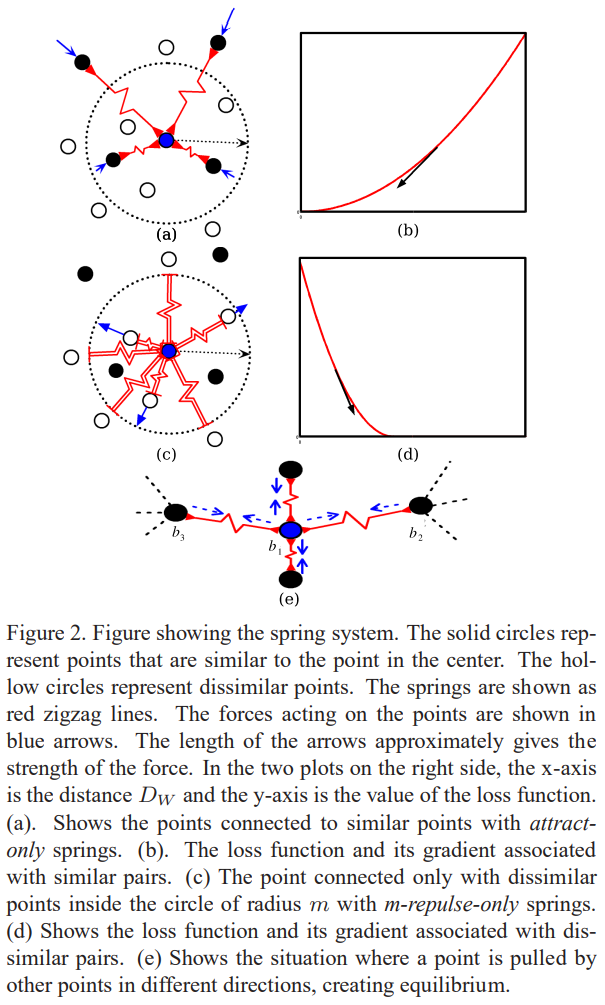
综上，得到最终的损失函数：

即正样本对时，样本间距离越小越好；负样本对时，样本间距离在阈值下越大越好。训练时，采用孪生网络，理想情况下，正负样本对之间进行”顶级拉扯”，相互作用力达到动态平衡。

Triplet loss

论文文献：FaceNet: A Unified Embedding for Face Recognition and Clustering

参考博客：Triplet Loss and Online Triplet Mining in TensorFlow

文章提出了triplet loss，主要用于学习人脸的向量表示，该损失函数的优势在于能够对输入的样本对进行更加细致的建模，对输入的差异性进行了度量，以学习到更好的向量表示。

目标：希望具有相似标签的样本，在编码空间里距离更近；而不同标签的样本，在编码空间里距离较远。

文章定义输入的三元组为，分别表示为锚点、正样本、负样本，则损失函数定义为：

通过优化该损失函数，使得，而，由于的存在，避免了退化解(否则直接时损失最小)，且能够限制正负样本对之间的相互关系(平衡模型训练难度和分类效果)。

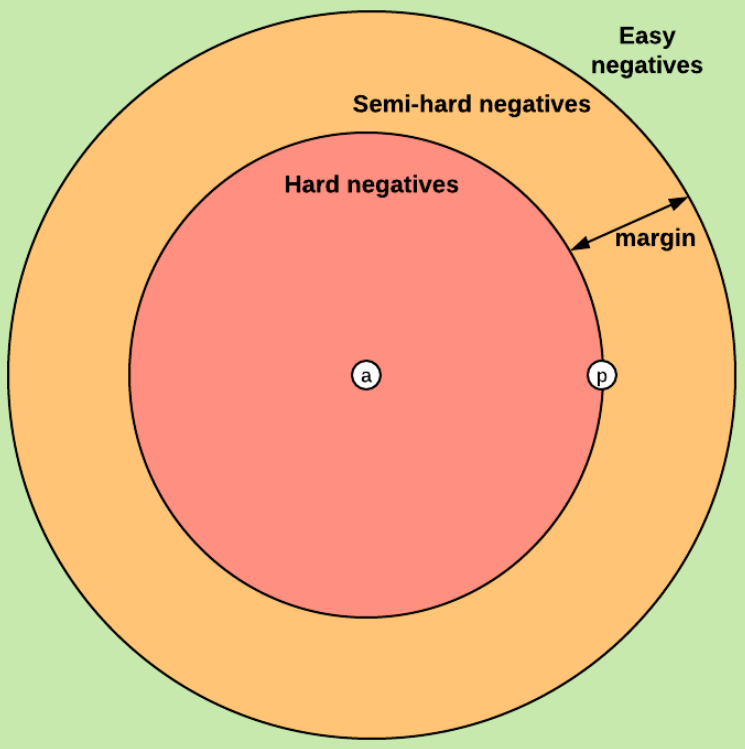
如上图，文章将三元组样本分为三类：

easy triplets：，即满足
hard triplets：负样本离锚点的距离小于正样本离锚点的距离，即
semi-hard triplets：正样本离锚点的距离小于负样本离锚点的距离，但未满足的限制，即

三元组样本的选择，会极大的影响模型效率(类似于hard sampling的那一套)。在FaceNet中，采用随机的semi-hard triplets的方法进行训练。

Noise Contrastive Estimation

论文文献：

Noise-contrastive estimation: A new estimation principle for unnormalized statistical models

A fast and simple algorithm for training neural probabilistic language models

参考博客：

Noise Contrastive Estimation

对比学习（Contrastive Learning）综述

语言模型通常假设所有可能的句子服从一个概率分布，每个句子出现的概率加起来为。通常把句子看成由个单词组成的序列，希望计算概率来得到句子出现的概率。基于链式法则，可以得到：

由上式可知，计算每个单词的条件概率计算量很大，故引入马尔可夫链的假设，即当前单词出现的概率仅与它前面出现的个词有关，称为模型，由此模型简化为：

在机器学习中，我们通常使用softmax函数来预测单词的条件概率：

其中，为单词的上下文，为分数函数，表示与上下文的匹配分数。为当前词库中所有单词的分数累加，称为配分函数或归一化因子，其计算量很大。

最大似然估计

先引入最大似然估计优化参数，假设单词服从数据分布，则对数似然函数可写为：

计算梯度：

上式能转换的原因是：，为所有词库中的单词，该单词的概率由产生，即，与分布不相关，故可以转换。专注于可得：

由此可得：

上式无法避免对的计算，计算量依旧复杂。

NCE

NCE将多分类问题转换为二分类问题，并引入噪声数据进行对比，并通过优化损失函数来估计模型参数和归一化常数。即希望分类器能够对数据样本和噪声样本进行二分类，由此学习到数据分布和噪声分布样本之间的区别，从而发现数据中的一些特性。

假设正样本来自特定上下文的数据分布，标签，负样本来自噪声分布(简单起见，假设与上下文无关)，标签。在训练时，每次选用个正样本和个负样本，由此构成训练数据分布。则可得：

由此，计算后验概率：

其中，，同理可得：

NCE不直接计算，而是将作为一个可训练的参数来估计，即，为原始的参数，则不依赖于，对于不同的上下文，存在不同的，即：

其中，，引入最大对数似然估计优化参数，则对数似然函数可写为：

计算梯度：

分别计算上式中的两部分：

由此可得：

若仅对求导，则可得：

当，则：

上式趋近于，说明当负样本和正样本数量之比越大，那么NCE对于噪声分布的依赖程度也越小，且当增大时，NCE梯度趋近于MLE梯度，这也是使用NCE成功的根本原因。

当上下文语境数量较大时，模型参数的数量也会变大，论文文献发现直接设置也能较好工作。

InfoNCE

论文文献：Representation Learning with Contrastive Predictive Coding

参考博客：Noise Contrastive Estimation 前世今生——从 NCE 到 InfoNCE

文章提出一种称为CPC的方法，通过无监督任务学习高维数据的特征表示，该方法根据上下文预测未来或缺失的信息。

目标：通过无监督表征学习，希望数据的表征不仅能尽可能保留原信号的信息，并且能具有很好的预测能力，即希望模型能学习到无标签数据本身的高维信息，并对下游任务产生帮助。

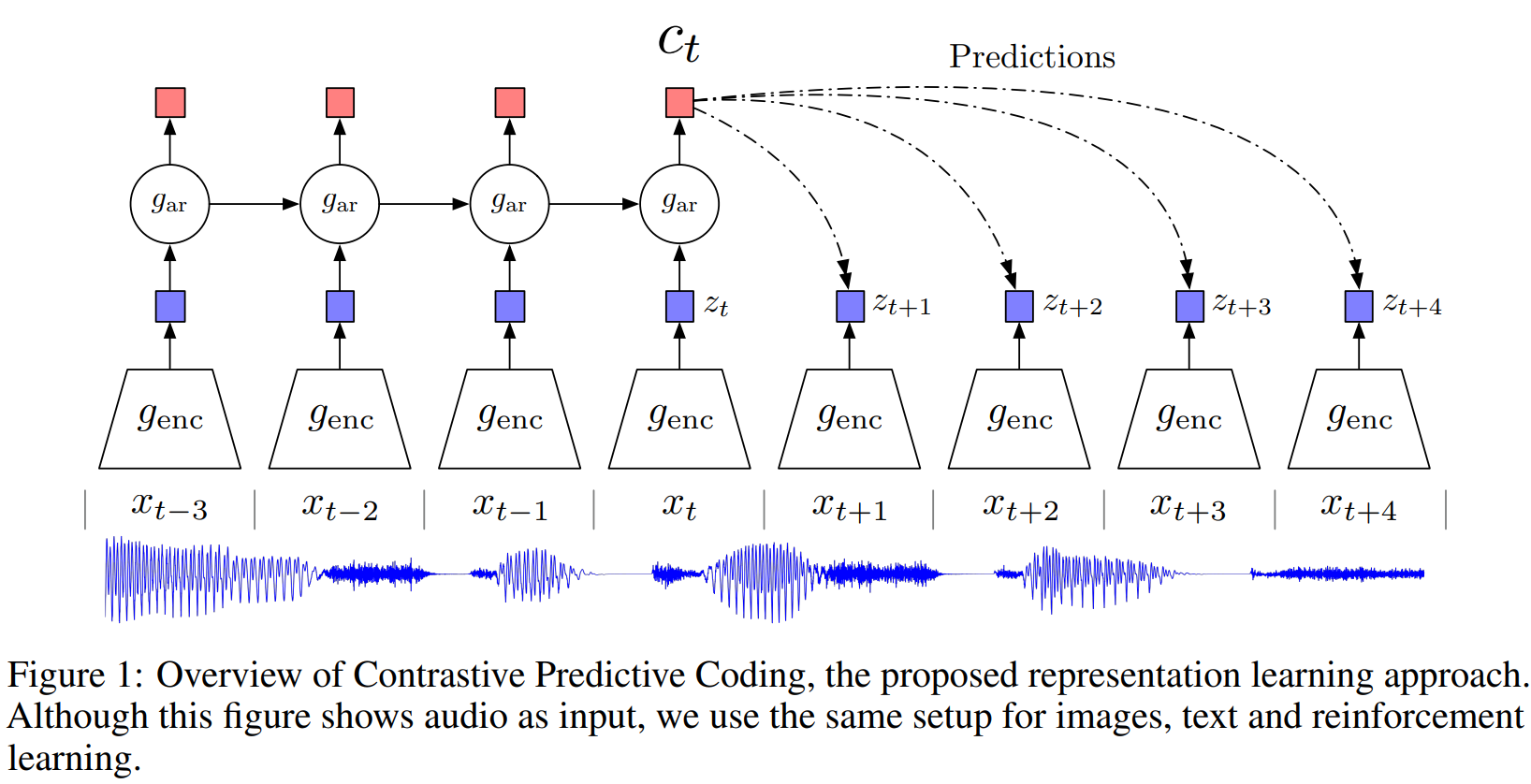
上图为CPC的结构图，传统方法是直接根据上下文预测个时刻后的数据，即建模生成模型，但该方法类似于细节重建，忽略了相互之间的关系；故引入互信息，即通过最大化当前上下文和时刻后的数据之间的互信息来构建预测任务。其中互信息的定义为：

我们无法知道联合分布，因此要最大化，就需要最大化。该比例定义为密度比，根据NCE提供的思路，相当于，即想得到的目标函数；而相当于，即用来进行对比的噪声。由此转换为二分类问题：

正样本：，即根据当前上下文所做出的预测数据，标签为；
负样本：，即跟当前上下文无必然关系的随机数据，标签为；

假设输入样本为，其中包含一个正样本和个负样本，故需要训练一个二分类模型区分正负样本对，则“成功分辨出每个正负样本的能力”等价于“根据预测的能力”。假设为正样本对，则最大化模型成功分辨出每个正负样本的概率：

上式相当于将位置给mask，最大化上式等价于最大化，即最大化和的互信息。CPC选用余弦相似度量化分数，故：

我们可以发现，上面两个式子的目标具有一致性，即：

所以，最终的InfoNCE损失函数为：

同时，文章证明最小化InfoNCE等价于最大化和的互信息下界，其证明如下：

You got a dream, you gotta protect it.