
原始Word2Vec的细节
Word2Vec通过最大化目标函数来使得拉近相似的word vectors
为什么使用两个vector:数学上更容易进行优化,可以在最后对两个vector进行平均得到一个vector。
模型变体:
Skip-gram model:从给定的center word预测context wordsContinuous Bag of Words:从一系列的context words中预测center word
原始Word2Vec的优化问题
虽然使用随机梯度下降SGD更新,但仍存在两个问题导致模型效率低下。
- 每次梯度更新时,仅更新
window中的word vector,但计算梯度时计算的整个参数矩阵,如果这个word未出现在window中,其偏导为0,则梯度矩阵非常稀疏; - 目标函数中计算条件概率时采用
softmax函数,其中分母计算所有context word与center word的相似度得分计算并求和。
解决方案:
针对稀疏矩阵,可以使用稀疏矩阵去更新特定的
embedding;或者使用hash映射到具体的word vector。针对
softmax函数计算量过大。解决方案包括:将常见词组作为一个
word;少采样常见词;Hierarchial Softmax(通过构建Huffman tree,复杂度由变为);negative sampling采用negative sampling
其主要思想为:训练一个二元逻辑斯蒂回归,去判断一对
word对是否是正负对(其中,center word跟真实context word为正对,center word跟随机采样的word为负对,希望正对相似度的概率更大,而负对相似度的概率更小)。之前的
skip-gram model可以看作是希望最大化,而negative sampling是希望最大化,而最小化,其中分别是的真实context word与随机context word。其总的损失函数为:
其中,对于
center word,希望context word与为正对,希望不是context word的与为负对,为采样的概率分布。最大化等价于最小化下式:为了平衡高频词和低频词的影响,取,其中为
unigram分布(即按词频比作为其概率分布),指数部分的是为了平衡词频的影响,而则是重新归一化为概率分布。由此,对
word vector进行更新,得到的式子如下:
如何构建共现矩阵?
word-document co-occurrence matrix:假设同一篇文章中出现的单词有可能互相关联,元素表示word出现在文章的次数。window-based word-word co-occurrence matrix:利用定长窗口统计窗口中word与word同时出现的次数。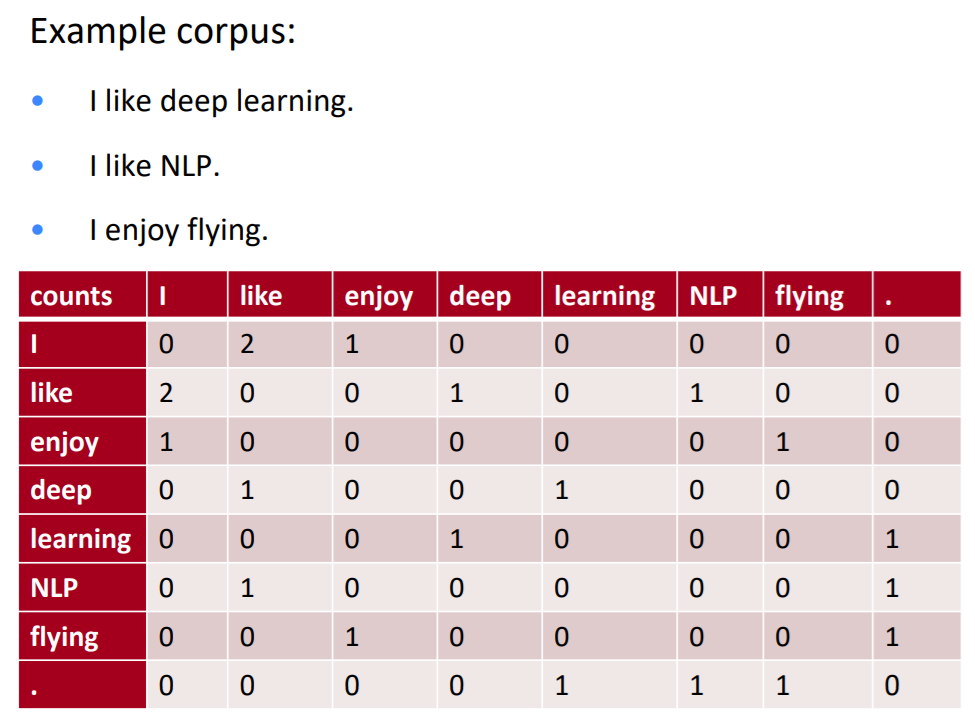
可能存在的问题:随着语料库的增加,维度过高,存储占用过大;存在稀疏性问题,模型不够鲁棒。
解决方法:
使用低维度的
vector,仅保存最重要的一些维度,构建dense vector;count based model的经典工作SVD:通过统计数据得到co-occurrence matrix,再对进行奇异值分解得到,为了减少尺度并尽量保留有效信息,选取对角矩阵中最大的个值。
Count based和direct prediction的比较
Count based(SVD):优点:训练快速,且有效利用了统计信息;
缺点:偏向于高频词,仅能概括
word的相关性。direct prediction(Word2Vec):优点:在其他任务上效果较好,且可以概括比相关性更复杂的信息;
缺点:受限于语料库的大小,对统计信息利用不够充分。
GloVe
结合
Count based Model和Direct Prediction Model的优势。优点:训练更快;可扩展到大型语料库;在小的语料库和
vector上也有较好的效果。
定义一个矩阵,其中表示word出现在word的context中的次数,则表示出现在word的context中的所有word的次数,表示word出现在word的context中的概率。
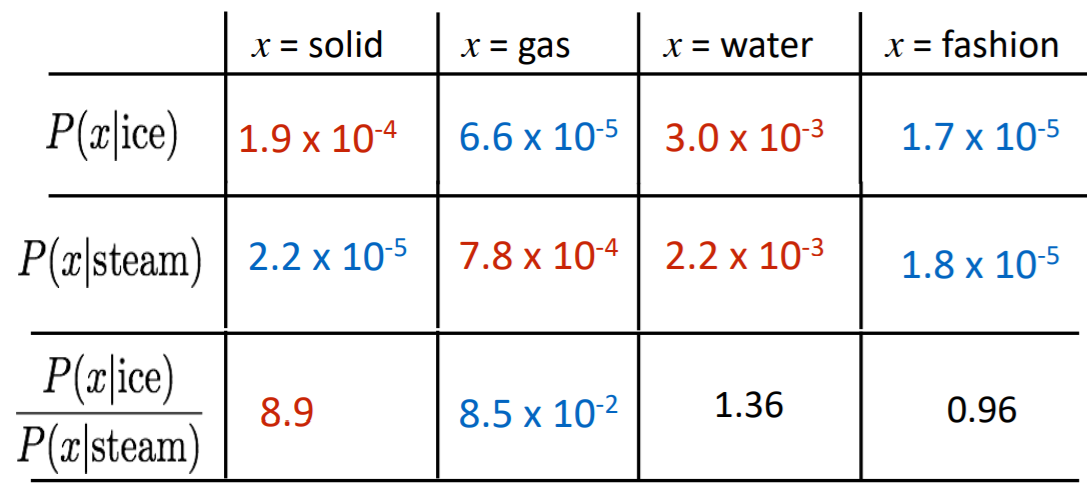
引入额外的word,比较共现概率的比值,发现如下的规律:
| 相关 | 不相关 | |
|---|---|---|
| 相关 | 接近1 | 很大 |
| 不相关 | 很小 | 接近1 |
由上表可知,能够反映word之间的相关性。
怎样在词向量空间中计算共现概率的比值?
假设对于
word vector,模型函数用来计算共现概率的比值,式子如下:其中,表示想要比较的
word vector,而表示其它的word vector。由于向量空间为线性空间,为了计算线性空间中的相似性,假设是
word vector作差的形式,则:上式左边为矢量,而右边为标量,通过选择矢量的点积来将矢量转化为标量形式,则:
上式左边为差,右边为商,通过选取来进行关联,得到:
由上式,我们希望,即,考虑
word-word co-occurrence共现矩阵的对称性,希望,但,引入两个偏置项平衡对称性,希望得到:则理想情况下,希望上式左右两部分接近,故目标函数为:
考虑
co-occurence word的出现次数的影响,加入作为权重,故最终目标函数为:其中,权重项需要满足如下条件:
- (如果两个
word没有共现,则权重为0); - 为非减函数(两个
word共现次数越大,权重不减); - 对于较大的,不能取过大的值(避免一些
word(比如,‘的’)共现次数较大,但其重要性较低)。
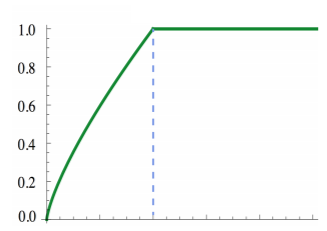
文中定义,其图像如下:
- (如果两个
参考文献:
CS224N笔记(二):GloVe - 知乎 (zhihu.com)
cs224n学习笔记L2:word vectors and word senses_三七的博客-CSDN博客