You got a dream, you gotta protect it.

0%

课程学习-CS224n-Lecture 1 Introduction and Word Vectors

发表于 更新于 分类于 Valine： 本文字数： 2.5k 阅读时长 ≈ 2 分钟

如何表示一个单词的含义

  • 建立所有同义词和下义词的词库

    如WordNet，一个单词的含义由它的同义词集合和下义词集合定义。

    缺点：某个单词只在特定语义下跟其他词为同义词；且词汇的新含义很难被包括；定义较为主观且需要人为整理；难以量化单词之间的相似程度。

  • 使用离散的符号表征单词

    传统的NLP将每个词表征为一个one-hot向量。

    优点：可以无限增添数据，构建一个足够大的词空间。

    缺点：词向量的维度就是单词的数量，过于庞大；所有向量正交，无效有效计算相似度。

    希望：能够理解不同单词之间的相互关系。

  • 通过上下文去表征单词

    背景：一个单词的定义往往由由它附近的单词决定。

    定义一个以单词为中心的定长窗口，该词称为center word，窗内其他词称为context，希望通过这些词去构建center word的有效表示。由此对每个单词构建一个word vector(大多数元素不为0且维度较小，也称为word embedding/representation)，希望相似的上下文，其word vector也相似。

如何得到word vector

Word2Vec

思想：已知有一个足够大的语料库，希望每个单词在一个固定的词汇表中被表征为一个向量。具体做法是通过扫描文本中的每个位置 t (每个位置 t 具有一个center word c 和一个context words o )， c 和 o 的word vector的相似性使用给定 c 条件下 o 的概率来表示(反之亦可)，初始时word vector为随机向量，通过不断调整word vector使得这个概率最大化(就是希望两者之间的相关性大)。

对于一个句子，其中每个单词 w 使用两个向量表示： (v_w,u_w) 分别表示该单词作为center word和context word的向量。

  • Skip-Gram model

    求context word相对于center word的条件概率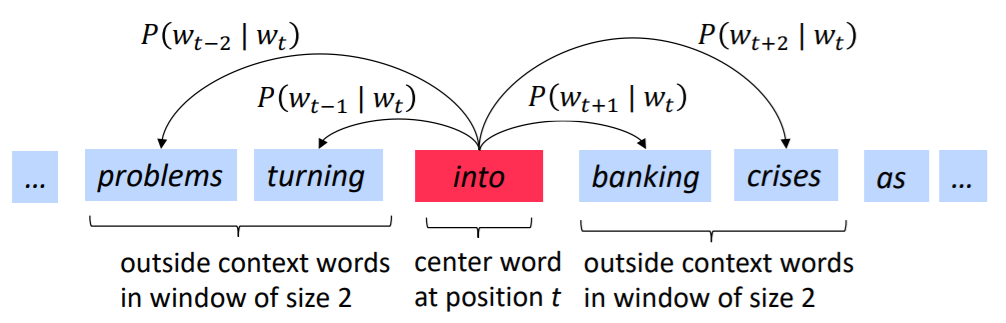

    则对于每个位置 t=1,…,T ，给定center word w_j ，以一个固定长度为 m 的窗口去预测context words。

    则总的似然函数为：

    L(\theta) = \prod_{t=1}^{T}\prod_{-m\le j\le m,\ j\ne0}P(w_{t+j}|w_t;\theta)

    由此得到总的目标函数(负对数似然函数)：

    J(\theta) = -\frac{1}{T}\log L(\theta) = -\frac{1}{T}\sum_{t=1}^{T}\sum_{-m\le j\le m,\ j\ne0}\log P(w_{t+j}|w_t;\theta)

    通过最小化目标函数，等价于最大化预测准确率。单个context word和center word的条件概率写作softmax形式：

    P(o｜c) = \frac{\exp(u_o^Tv_c)}{\sum_{w\in V}\exp(u_w^Tv_c)}

    其中， u_o^Tv_c 越大，等价于概率越大。通过对损失函数求导，得到：

    \begin{aligned} \frac{\partial \log P(o|c)}{\partial v_c} &= \frac{\partial [u_o^Tv_c - \log(\sum_{w\in V}\exp(u_o^Tv_c))]}{\partial v_c}\\ &= u_o - \frac{\sum_{x\in V}\exp(u_x^Tv_c)u_x}{\sum_{w\in V}\exp(u_w^Tv_c)} \\ &= u_o - \sum_{x\in V}P(x|c)u_x \end{aligned}

    由上式可以看出，梯度与实际的context word与预期的context word的加权求和有关。

    使用gensim可进行word vector的相似度计算、PCA可视化等

参考文献：

  • CS224N笔记(一)：Word Vector - 知乎 (zhihu.com)
相关文章