
动机
- 目前大多数编辑生成图像的方法都是通过利用标准GAN训练后隐式获得的潜在空间解纠缠特性来实现部分控制,不能显式地设置某些属性地值;
- 最近提出的方法可以显式地控制人脸属性,其利用可变形地3D人脸模型来使得GAN具有细粒度控制能力,但不能扩展到人脸领域外。
贡献
本文的方法
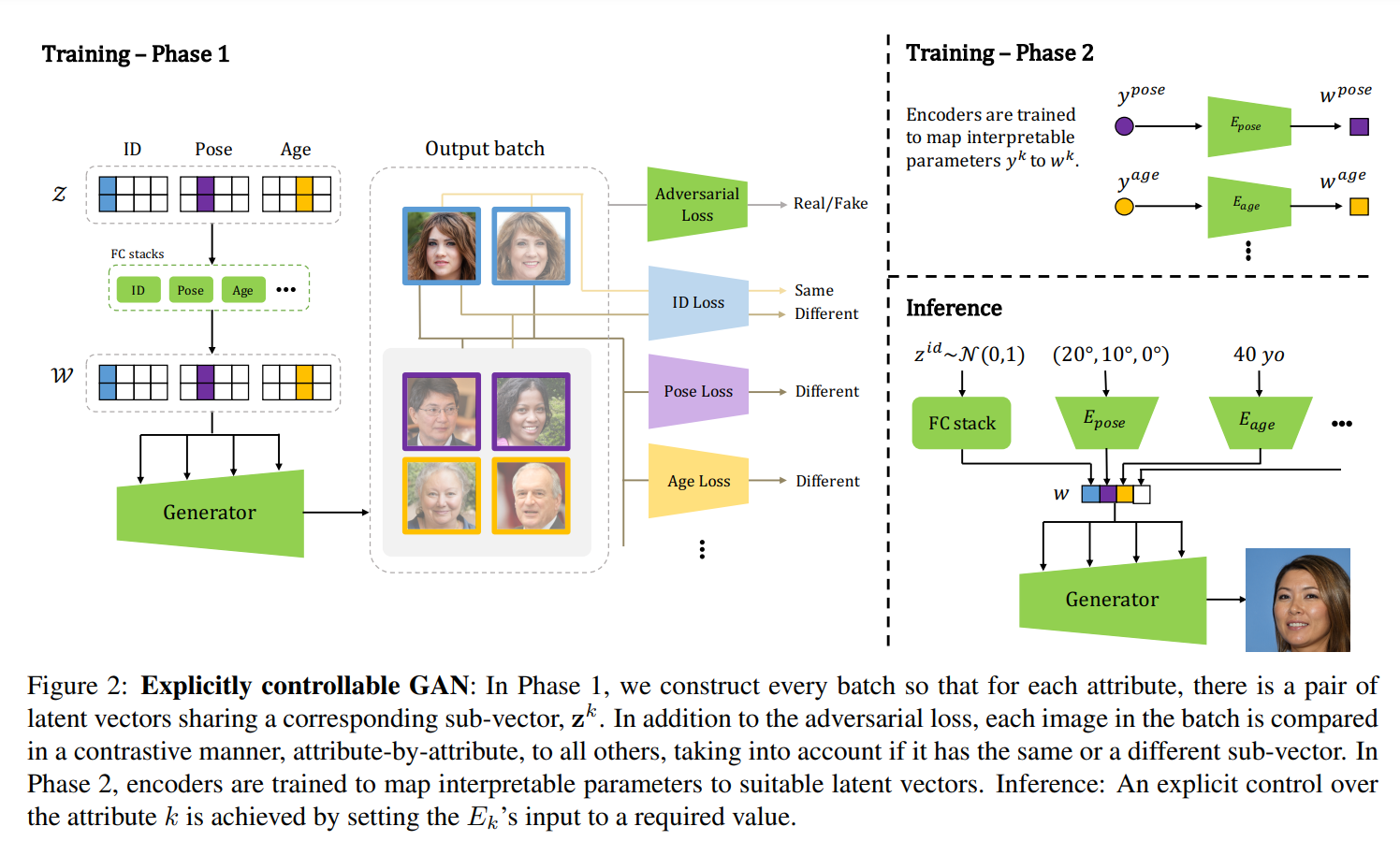
如上图,本文的方法包含两个阶段:
- 利用对比学习解纠缠:训练具有显式解纠缠特性的GAN,由此将潜在空间划分为子空间,每个子空间编码不同的图像属性;
- 可解释的显式控制:对于每个属性,一个编码器被训练来映射控制参数值到潜在的子空间,由此可以显式地控制每个属性。
利用对比学习解纠缠
本文方法基于StyleGAN2,将隐空间和均划分为个子空间,为控制的属性数量,除了最后一个子空间代表不可控的属性,每个子空间认为跟一种属性相关,由此得到和,即为生成器的输入。
定义表示从隐向量生成的图像,表示batch_size为的隐向量,则因式分解的对比损失定义为:
其中是属性的对比损失,定义每个属性的对比损失为:
其中,表示的第个子向量,是属性的距离函数,是与相同和不同子向量相关的各属性阈值,是常数,根据相同和不同的损失分量的数量对损失进行归一化,即:
实验中,对于每个训练批,作者设置共享一个子向量的隐向量对,即对于一个属性,会创建一对隐向量和,其中且。例如假设生成图像中的和共享相同的,则会惩罚与的ID不相同和或的ID与其它图像的11ID相同,而其它属性的损失会惩罚和所有其它图像的相似。
为了能够控制生成图像的特定属性,假设可微函数将图像映射到一个维的特征,并假设属性值相似的投影图像之间的距离很近,而属性值不同的投影图像之间的距离很远,这些要求被大多数用于分类或回归损失训练的神经网络所满足。将两幅图像和之间的第个属性的距离定义为它们在相应嵌入空间中的距离:
其中是距离函数,如cosine distance.
可解释的显式控制
训练一个编码器来显式控制特定的属性,其中是人类可解释的输入。对于一个训练好的解纠缠GAN,训练个编码器,每个编码器对应一种属性。这样在推理时,可以随意组合,并决定其由显式控制,或者是由采样。
训练编码器时,随机采样,由此得到,并由得到预测的属性值,由此得到一组对应的关系,由此可以训练编码器。
部分实验结果





