You got a dream, you gotta protect it.

0%

论文阅读-contrastive-learning-Contrastive Learning with Hard Negative Samples

发表于 分类于 Valine： 本文字数： 6.8k 阅读时长 ≈ 6 分钟
用困难的负样本进行对比学习-ICLR2021

动机

  • 现有的对比学习方法都致力于研究正对方面的选择(即不同的数据增强方法)，负对的选择的研究少得多；

  • 作者认为，类似度量学习，学习对比表征也会从hard negative samples中受益，使用hard negatives的关键挑战是对比方法必须保证无监督，这使得采用现有的使用标签信息的负采样策略失效。

贡献

  • 构建了一个用于对比表征学习的hard negative pairs的采样分布(偏好当前表征非常相似的负对)，并在缺乏真正不相似信息情况下(无监督情况下)提出了一个有效的采样策略；

  • 从理论上分析了目标函数和最优表征的性质，其将相似的输入放在紧密的簇类中，同时将不同簇类分隔得尽可能远；

  • 实验上观测到所提出的采样方法提高了图像、图、文本数据的下游任务性能。

对比学习设置

对比表征学习希望学习一个嵌入函数 f:\mathcal{X}\rightarrow \mathbf{S}^{d-1}/t ，它将一个观测 x 映射到半径为 1/t 的超球面 \mathbf{S}^{d-1}/t\in \mathbb{R}^d 上的一点，其中 t 是温度尺度超参数。

假定一组表示语义内容的离散潜在类 \mathcal{C} ，则相似对 (x,x^{+}) 则具有相同的潜在类别。用 \rho(c) 表示潜在类 c\in \mathcal{C} 的分布，定义联合分布 p_{x,c}(x,c)=p(x|c)\rho(c) ，边缘分布 p(x) 简写为 p ，并假定 \text{supp}(p)=\mathcal{X} 。假设 \rho(c)=\tau^{+} 是均匀分布，而 \tau^{-}=1-\tau^{+} 表示另一类的概率，而 \tau^{+} 是未知的类先验，故需要认定为超参数或被估计。

设 h:\mathcal{X}\rightarrow \mathcal{C} 为对输入赋予类别的真实的潜在假设(可以理解为一个分类器)，使用 x\sim x^{\prime} 表示标签相等的关系 h(x)=h(x^{\prime}) ， p_{x}^{+}\left(x^{\prime}\right)=p\left(x^{\prime} \mid h\left(x^{\prime}\right)= h(x)\right) 表示与 x 有相同标签的数据点的分布， p_{x}^{-}\left(x^{\prime}\right)=p\left(x^{\prime} \mid h\left(x^{\prime}\right) \neq h(x)\right) 表示与 x 不同标签的数据点的分布， x \sim p 表示从 p 中采样一个数据点。

对于每个数据点 x\sim p ，用于学习表征 f 的噪声对比估计(NCE)损失函数使用一个与 x 相同标签的正例 x^{+} 和不同标签( h(x_i^-)\ne h(x) )的负例 \{x_i^+\}_{i=1}^N (采样自 q )：

\mathbb{E}_{x \sim p, \quad x^{+} \sim p_{x}^{+} \\ \left\{x_{i}^{-}\right\}_{i=1}^{N} \sim q}\left[-\log \frac{e^{f(x)^{T} f\left(x^{+}\right)}}{e^{f(x)^{T} f\left(x^{+}\right)}+\frac{Q}{N} \sum_{i=1}^{N} e^{f(x)^{T} f\left(x_{i}^{-}\right)}} \right].

通常取 Q = N ，即负样本数。负样本分布 q 经常被选择为边缘分布 p ，或者在实践中是它的经验近似。本文的问题是：是否有更好的方法来选择 q 。

困难负样本采样

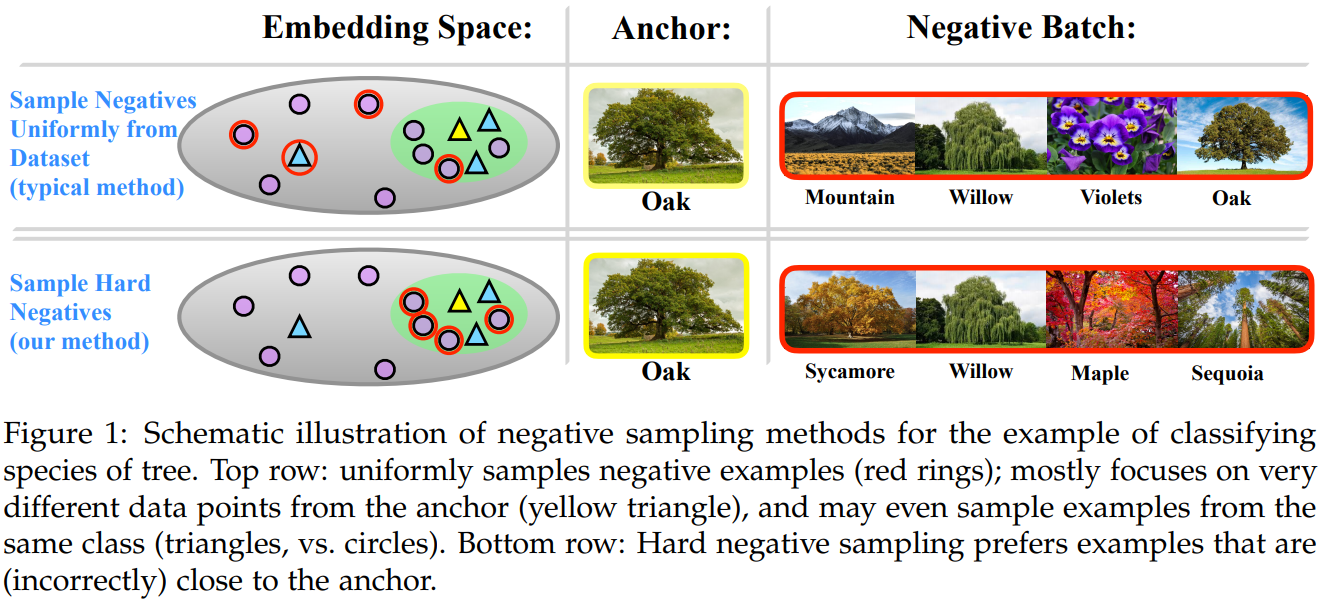
对于什么是好的负样本，本文给出两个定义：

  • q 应该只采样标签跟锚点 x 不同的负样本 x_i^- ；
  • 最有用的负样本是那些被认为与锚点相似的样本。

即如上图，需要选择与锚点不同标签的负样本，且在嵌入空间与锚点相近的负样本在训练期间能提供更显著的梯度信息。在对比学习中无监督，则定义 1 是不可能做到的，本文则提出了一种方法，在坚持定义 1 时，结合额外的概念hardness，hardness是一个trades-off(在hard negatives提升学习表征和错误的negatives损害性能之间，因为最困难的点是在嵌入空间中离锚点最近的点，但离得近的点有较高的倾向有相同的标签，如果没有去除假负样本会造成损害)。当hardness完全调低，则得到Debiased Contrastive Learning中的方法，即近似支持定义 1 ，而不支持定义 2 ，此外本文希望设计一种有效的采样方法，使得在训练期间不会增加额外的计算开销。

提出的困难负样本采样方法

首先在 \mathcal{X} 上设计一个分布 q ，它依赖于嵌入 f 和锚点 x 。从 q 采样一个batch的负样本 \{x_i^+\}_{i=1}^N ，则对应的分布 q_{\beta}^{-} 定义为：

q_{\beta}^{-}\left(x^{-}\right):=q_{\beta}\left(x^{-} \mid h(x) \neq h\left(x^{-}\right)\right), \quad \text { where } \quad q_{\beta}\left(x^{-}\right) \propto e^{\beta f(x)^{\top} f\left(x^{-}\right)} \cdot p\left(x^{-}\right)

其中 \beta\ge 0 ， q_{\beta} 的指数部分是均值方向为 f(x) ，集中参数(concentration parameter)为 \beta 的非归一化von Mises–Fisher分布。对于 q_{\beta}^{-} ，在 \{h(x)\ne h(x^{-})\} 的条件下保证了 (x,x^{-}) 是不同的潜在类别(定义 1 )；集中参数 \beta 则控制了 q_{\beta} 上的权重点 x^{-} 与锚点 x 有较大内积(相似度)的程度(即上式中， e^{\beta f(x)^{\top} f(x^{-})}=(e^{f(x)^{\top} f(x^{-})})^{\beta} ，同时 p(x^{-}) 表示为负样本的概率，使得相似度大的负样本，其取值更大，则采样时更容易采到)。又由于 f 位于半径为 1/t 的超球面上，故有 \left|f(x)-f\left(x^{\prime}\right)\right|^{2}=2 / t^{2}-2 f(x)^{\top} f\left(x^{\prime}\right) ，故偏好有大内积的点等同于偏好有小欧氏距离平方的点。

为了实现一种实用方法，通过采用Pull-learning的观点重写这个分布，则得到(类似全概率公式)：

q_{\beta}\left(x^{-}\right)=\tau^{-} q_{\beta}^{-}\left(x^{-}\right)+\tau^{+} q_{\beta}^{+}\left(x^{-}\right)

其中 q_{\beta}^{+}\left(x^{-}\right)=q_{\beta}\left(x^{-} \mid h(x)=h\left(x^{-}\right)\right) \propto e^{\beta f(x)^{\top} f\left(x^{-}\right)} \cdot p^{+}\left(x^{-}\right) ，则可以得到负采样的分布 q_{\beta}^{-}\left(x^{-}\right)=\left(q_{\beta}\left(x^{-}\right)-\tau^{+} q_{\beta}^{+}\left(x^{-}\right)\right) / \tau^{-} ，其有两个可跟踪的分布构成，因为有从 p 采样的样本，且能够近似从 p^{+} 采样的样本(使用语义不变性转换)。

由上述，可以通过从 q_{\beta} 中生成样本，且能使用rejection sampling近似从 q_{\beta}^{+} 采样的样本，但rejection sampling涉及到在采样batch时增加一个额外的速度较慢的步骤。本文改写了对比损失，固定 Q 并使得 N\rightarrow \infty ：

\mathcal{L}(f, q)=\mathbb{E} \underset{x^{+} \sim p_{x}^{+}}{x \sim p}\left[-\log \frac{e^{f(x)^{T} f\left(x^{+}\right)}}{e^{f(x)^{T} f\left(x^{+}\right)}+Q \mathbb{E}_{x^{-} \sim q}\left[e^{f(x)^{T} f\left(x^{-}\right)}\right]}\right]

将 q=q_{\beta}^{-} 代入上式，则得到hardness-biased目标函数：

\mathbb{E}_{x \sim p\\ x^+\sim p_x^+}\left[-\log \frac{e^{f(x)^{T} f\left(x^{+}\right)}}{e^{f(x)^{T} f\left(x^{+}\right)}+\frac{Q}{\tau^{-}}\left(\mathbb{E}_{x^{-} \sim q_{\beta} }\left[e^{f(x)^{T} f\left(x^{-}\right)}\right]-\tau^{+} \mathbb{E}_{v \sim q_{\beta}^{+} }\left[e^{f(x)^{T} f(v)}\right]\right)}\right]

这个目标函数表明只需要估计期望 \mathbb{E}_{x^{-} \sim q_{\beta} }\left[e^{f(x)^{T} f\left(x^{-}\right)}\right] 和 \mathbb{E}_{v \sim q_{\beta}^{+} }\left[e^{f(x)^{T} f(v)}\right] ，可对采样自 p 和 p^+ 的样本使用经典的Monte-Carlo importance sampling：

\begin{aligned} \mathbb{E}_{x^{-} \sim q_{\beta} }\left[e^{f(x)^{T} f\left(x^{-}\right)}\right] &=\mathbb{E}_{x^{-} \sim p}\left[e^{f(x)^{T} f\left(x^{-}\right)} q_{\beta} / p\right]=\mathbb{E}_{x^{-} \sim p}\left[e^{(\beta+1) f(x)^{T} f\left(x^{-}\right)} / Z_{\beta}\right] \\ \mathbb{E}_{v \sim q_{\beta}^{+} }\left[e^{f(x)^{T} f(v)}\right] &=\mathbb{E}_{v \sim p+}\left[e^{f(x)^{T}f(v)} q_{\beta}^{+} / p^{+}\right] =\mathbb{E}_{v \sim p+}\left[e^{(\beta+1) f(x)^{T} f(v)} / Z_{\beta}^{+}\right] \end{aligned}

其中， Z_{\beta} ， Z_{\beta}^{+} 分别是 q_{\beta} 和 q_{\beta^{+} } 的配分函数，用经验项 \hat{p}(x)=\frac{1}{N} \sum_{i=1}^{N} \delta_{x_{i}^{-} }(x) ， \hat{p}^{+}(x)=\frac{1}{M} \sum_{i=1}^{M} \delta_{x_{i}^{+} }(x) (其中 \delta_{w} 是中心在 w 的Dirac delta function)来近似 p 和 p^+ ，而 Z_{\beta}=\mathbb{E}_{x^{-} \sim p}\left[e^{\beta f(x)^{r} f\left(x^{-}\right)}\right] 和 Z_{\beta}^{+}=\mathbb{E}_{x^{+} \sim p^{+}}\left[e^{\beta f(x)^{r} f\left(x^{+}\right)}\right] 可以得到如下的经验估计：

\hat{Z}_{\beta}=\frac{1}{N} \sum_{i=1}^{N} e^{\beta f(x)^{\top} f\left(x_{i}^{-}\right)}, \quad \hat{Z}_{\beta}^{+}=\frac{1}{M} \sum_{i=1}^{M} e^{\beta f(x)^{\top} f\left(x_{i}^{+}\right)}

文章建议重新调整目标函数的权重，而不是修改采样过程，文章只需要额外的两行代码而不需要额外的计算开销。

关于Hard Sampling的分析

此外，文章分析了Hard Sampling是在Marginal和Worst-Case Negatives之间的中间情况，并分析了在Worst-Case Negative情况下负样本在超球面的最优嵌入，见原论文part 4，相关证明略。

文章在part 6讨论了两个问题：

  • 是否更难的样本一定更好？

    不能设置过大的 \beta ，过大的时候靠近的样本，存在过多的假的负样本(与 x 是同类)

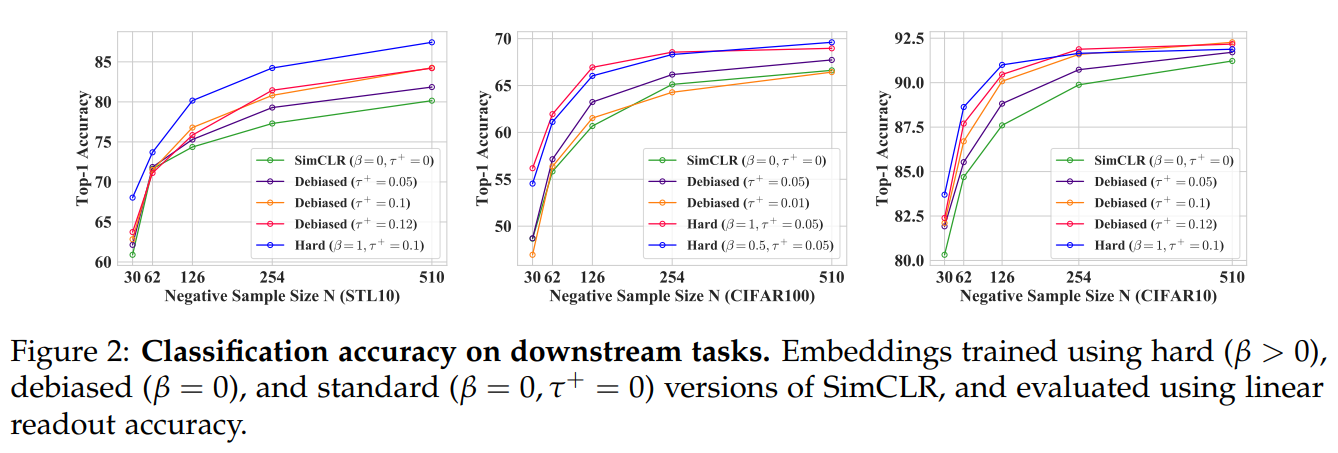
    将 \beta 设置为较大的值，则模型只关注最难的样本，但下图的实验显示更大的 \beta 并不一定会有更好的结果，且当在训练过程中使用真正的正对(绿色曲线，对于正对使用标签信息，对于负对不使用)，下游任务的性能随着 \beta 单调增加直至收敛。这说明，在 \{h(x)\ne h(x^-)\} 的条件下，使用真实的 p^+ 来修正采样与 x 具有相同标签的 x^- ，但实际使用一组数据增强来近似 p^+ ，则只能部分修正。对于大的 \beta ，这种情况会很偏向 x^- ，而 f(x^-) 接近 f(x) ，其中有许多与 x 有相同的标签，如果不纠正，将会对性能有害。

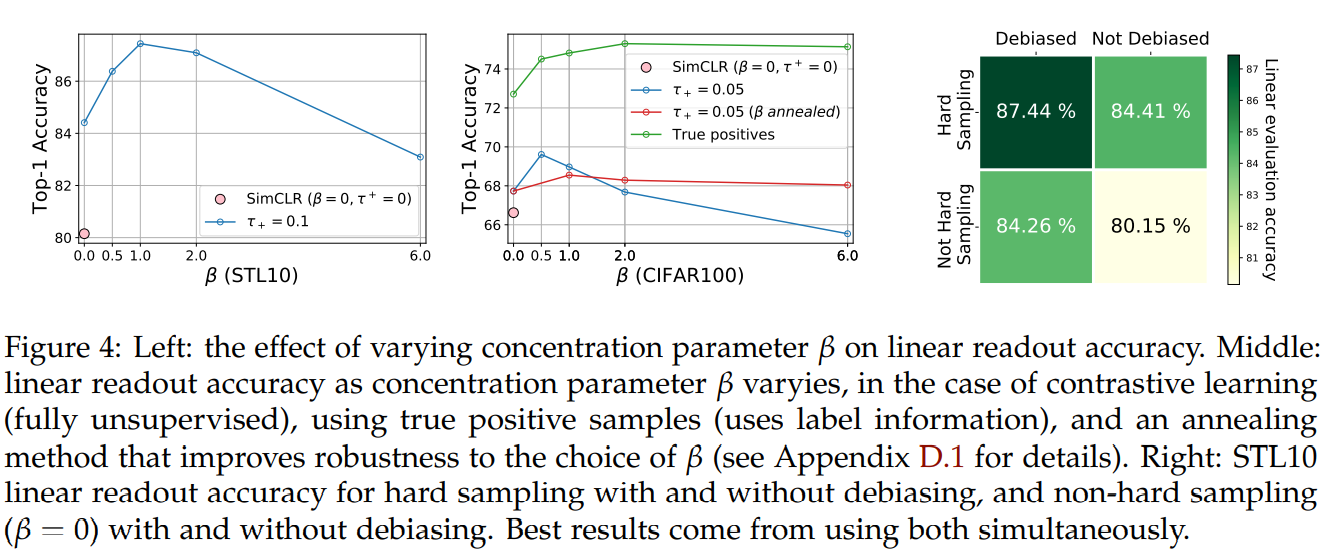
  • 避免错误的负样本会改善这个采样?

    称条件 \{h(x)\ne h(x^-)\} 为debiasing，用来避免错误的负样本，文章测量了这部分的作用。上图最右的图像显示了在hard sampling和均匀采样时，带debiasing都比不带debiasing好。

    下图比较了这四种情况下的正负对余弦相似度的直方图，hard sampling比均匀采样的重叠更少，能更好的权衡更高的不相似的负对和较少的相似的正对，对于带debiasing和不带debiasing的情况类似。

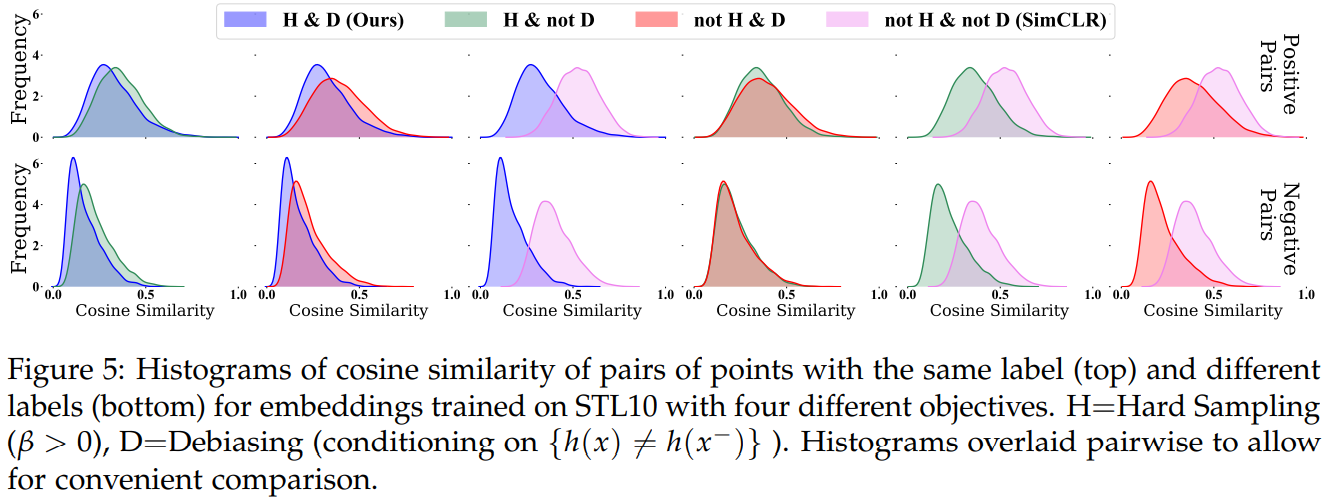
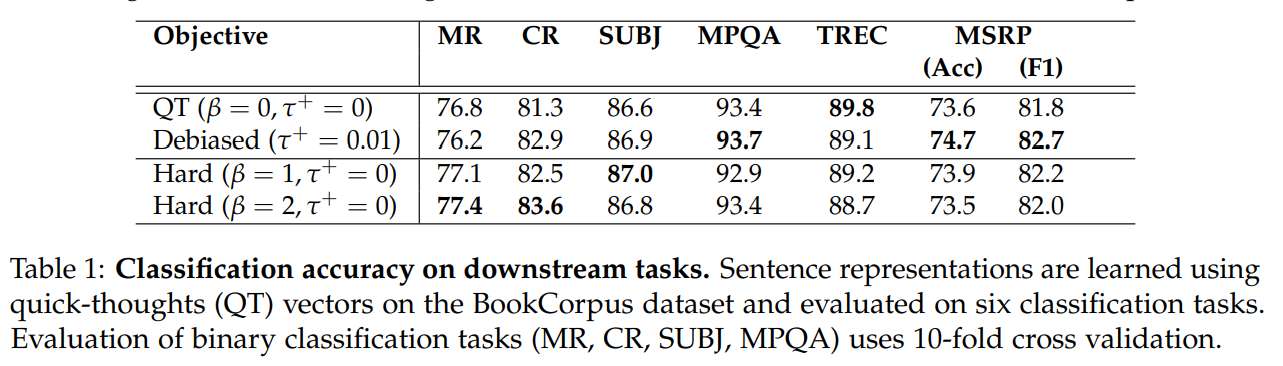
部分实验结果

图像表征：

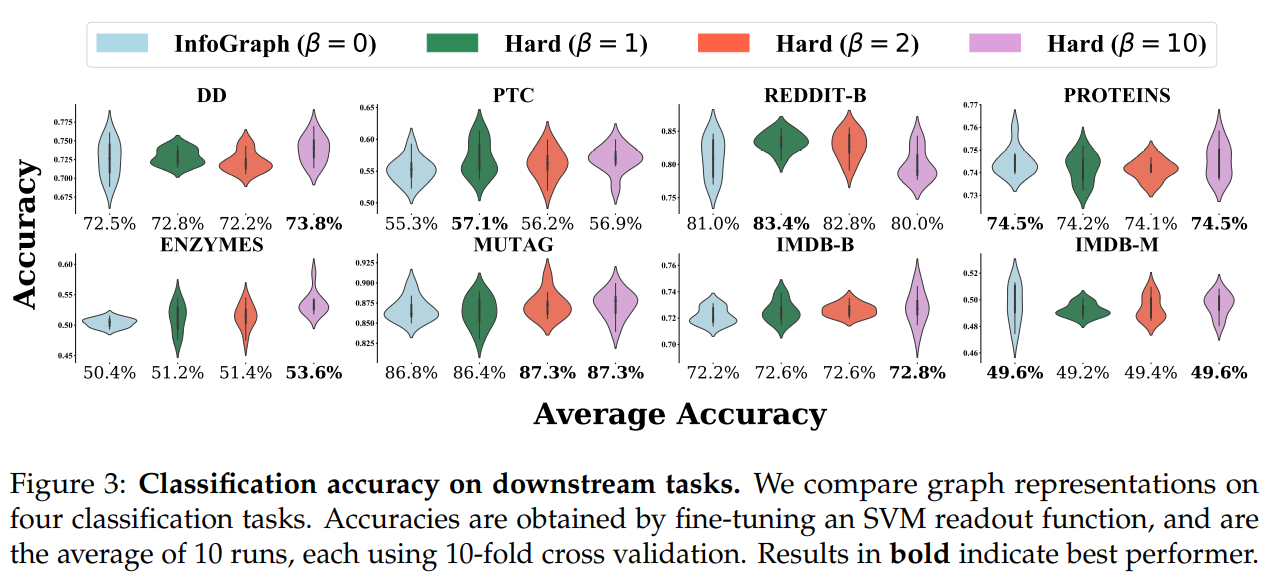
图的表征：

句子表征：

相关文章