
动机
- 扩散模型定义简单,训练效率高,但还没有方法显示其能够生成高质量图像。
贡献
- 提出了一种使用扩散概率模型(一种受非平衡热力学启发的隐变量模型)的图像合成方法;
- 发现了扩散模型的某种参数化与训练期间在多个噪声水平上的去噪分数匹配和采样期间的
annealed Langevin dynamics等价;
- 发现了模型的大部分无损编码被用于描述难以察觉的图像细节,证明了扩散模型的采样过程是一种渐进解码类型,可以解释为自回归解码的泛化。
扩散模型
扩散模型是一种形式为的隐变量模型,其中是与数据具有相同维度的隐变量,联合概率被称为反向过程,定义为从开始学习的高斯变换的马尔科夫链:
扩散模型与其他类型的隐变量模型的区别在于,近似后验,称为前向过程或扩散过程,被固定在马尔可夫链上,该马尔可夫链逐步将高斯噪声的方差以一种策略添加到数据中:
训练则通过优化负对数似然的变分上界,即:
前向过程方差可通过重参数化学习或者保持为常数作为超参数,反向过程的表达由中高斯条件的选择来保证。前向过程的一个显著特性是,它允许在任意时间步上以闭合形式对进行采样:定义,则:
因此,可以通过随机梯度下降法优化的随机项,进一步的改进是通过重写来减少方差:
上式利用距离去比较和正向过程的后验,其在条件下易跟踪:
所以,距离均是高斯分布之间的比较,故可用闭式表达式形式的Rao-Blackwellized方法代替高方差的Monte Carlo估计。
本文的方法
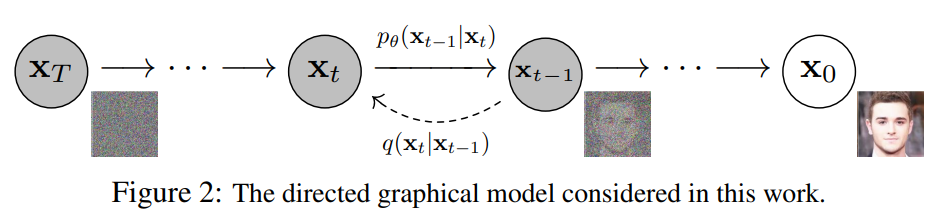
扩散模型可以看作是一种隐变量模型,在实现过程中包含了大量的自由度,如前向过程的方差,反向过程的模型结构和反向过程的高斯分布参数化。本文在扩散模型和去噪分数匹配之间建立了一种显式的联系,从而为扩散模型建立了一个简化的加权变分边界目标。
前向过程和
本文将前向过程方差固定为常数,故近似后验没有可学习参数,故是常数(因为,),可忽略。
反向过程和
对于,首先设置为未经训练的时间依赖常数,如或,第一种选择对于是最优的,第二种选择对于被设置为一个点来说是最优的,这是两种极端的选择,对应于具有单位方差的数据的反向过程的熵的上界和下界。
对于,基于如下的分析提出了一种参数化方法:对于,有:
其中是不依赖的常数,最简单的参数化是是一个模型,去预测前向过程的后验均值,通过上文的去扩展,即,则得到:
上式则显示了对于给定的必须预测,由于可以作为模型的输入,所以可以将参数化为:
其中是一个函数,旨在从预测。采样是通过计算(由推导),完整的采样过程类似带数据密度的可学习的梯度的Langevin dynamics,由上式的参数化,故简化为:
这类似于在多个噪声尺度(索引为)上的去噪分数匹配,由于上式等价于类似Langevin dynamics反向过程的变分边界,优化类似去噪分数匹配的目标等价于使用变分推断去拟合类似Langevin dynamics的采样链的有限时间边际。
总而言之,可以训练反向过程均值函数近似去预测,也可以去预测(也可以预测,但实验早期会导致较差的样本质量)。作者表明,预测类似于Langevin dynamics,且能够简化扩散模型的变分边界到一个类似去噪分数匹配的目标函数,注意它只是另一种的参数化方法。
数据缩放,反向过程解码器和
假设图像数据由线性缩放到,这保证神经网络反向过程从标准正态先验开始,在缩放一致的输入上操作。为了得到离散对数似然,将反向过程的最后一项设置为一个由高斯函数派生的独立的离散解码器:
其中是数据维数,上标表示提取一个坐标(可以合并一个更强大的解码器),类似于VAE的解码器和自回归模型的离散连续分布,本文的选择确保了变分边界是离散数据的无损编码长度,不需要在数据中添加噪声,也不需要在对数似然中纳入比例运算的Jacobian矩阵。在采样的最后,会得到无损的。
简化训练目标
由上述的推导,实验中使用以下变分边界的变体(有利于图像质量且更容易实现):
其中,属于区间,的情况对应于,前文离散解码器的定义中的积分近似于高斯概率密度函数乘以bin宽度(忽略和边缘效应),的情况对应于未加权的,类似于NCSN去噪分数匹配模型中使用的加权损失(没有出现,因为前向过程的方差是固定的)。
简化的目标函数不考虑前文推导的权重,与标准变分边界相比,加权变分边界强调重构的不同方面。本文实验设置使得简化目标降低对应小的损失项的权重,这部分训练网络去降噪,所以在更大的时,降低它们的权重有利于专注于困难的去噪任务。
训练过程和采样过程如下:

部分实验结果
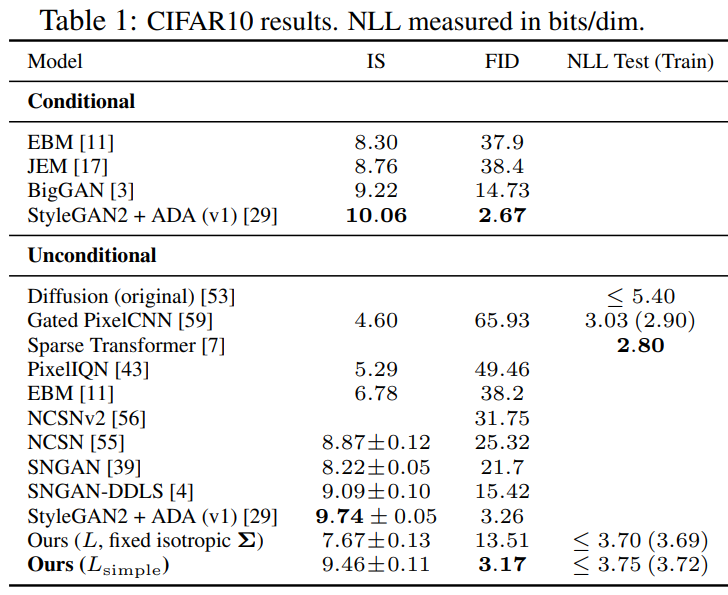
采样质量:
比较了IS,FID和负对数似然(无损编码长度),训练集的FID是,测试集的FID为。
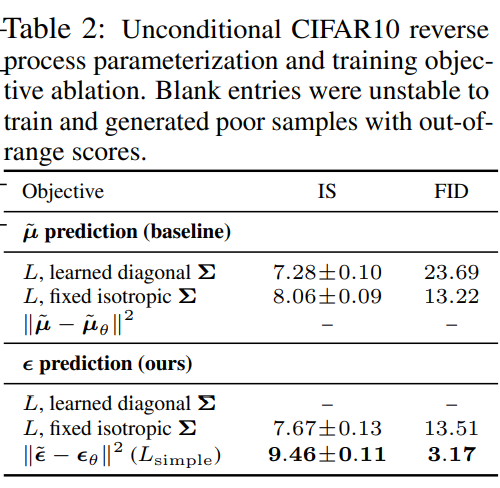
反向过程参数化和训练目标消融实验:
实验发现在基线模型中,适用于训练真正的变分约束;学习反向过程方差(将参数化的加入到变分边界中)会导致不稳定的训练;固定方差时预测比好;预测时,简化的变分边界有更好的样本质量。
渐进编码:
渐进有损压缩
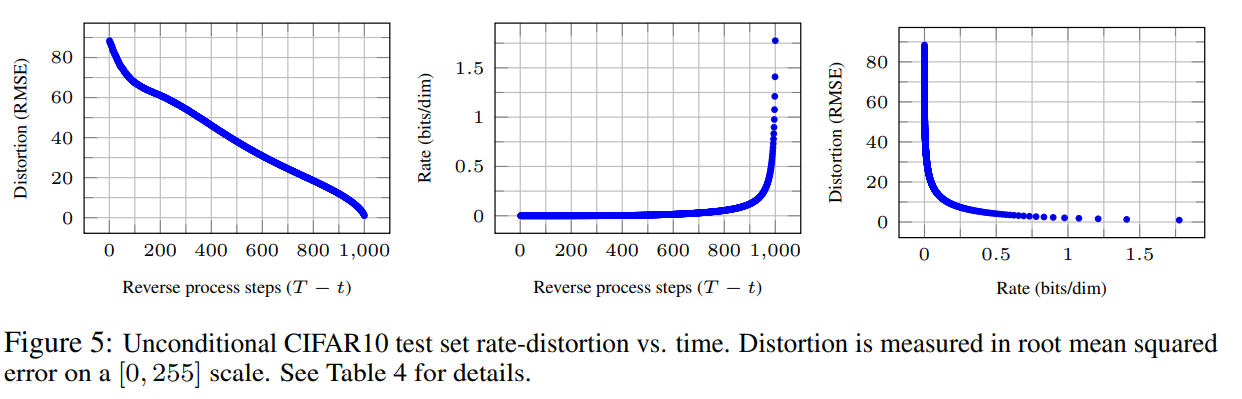
如下图引入一个渐进有损编码,去进一步探究模型的rate-distortion behavior。它假设访问一个过程,对于任意分布和,其中只有预先对接收方可用,平均使用大约bit去传输一个样本。

失真在率失真图的低率区域急剧下降,这表明大多数比特分配给了难以察觉的失真。
渐进生成
通过使用Algorithm 2采样反向过程,去预测。
下图显示按照反向过程去采样的结果,大尺度图像特征最先出现,细节最后出现。

下图显示了在不同时的随机预测,当很小时,几乎所有细节都被保留,当很大时,只有大尺度的特征被保留。

与自回归解码的联系
扩散模型的变分边界可以重写为:
作者证明在某些情况下,其等价于训练自回归模型。
插值:
将作为随机编码器,对于源图像,由和,然后对线性插值通过反向过程解码到图像空间。










