动机
- 现有的对比学习方法是通过减少正对特征之间的距离,增加负对之间的距离来训练的,这种方法依赖大的
batchsize、memeory bank或自定义的数据挖掘策略来处理负对;
- 现有的对比学习方法性能也严重依赖于图像的增强方法。
贡献
- 提出了一种新的自监督学习方法
BYOL,其不使用负对样本;
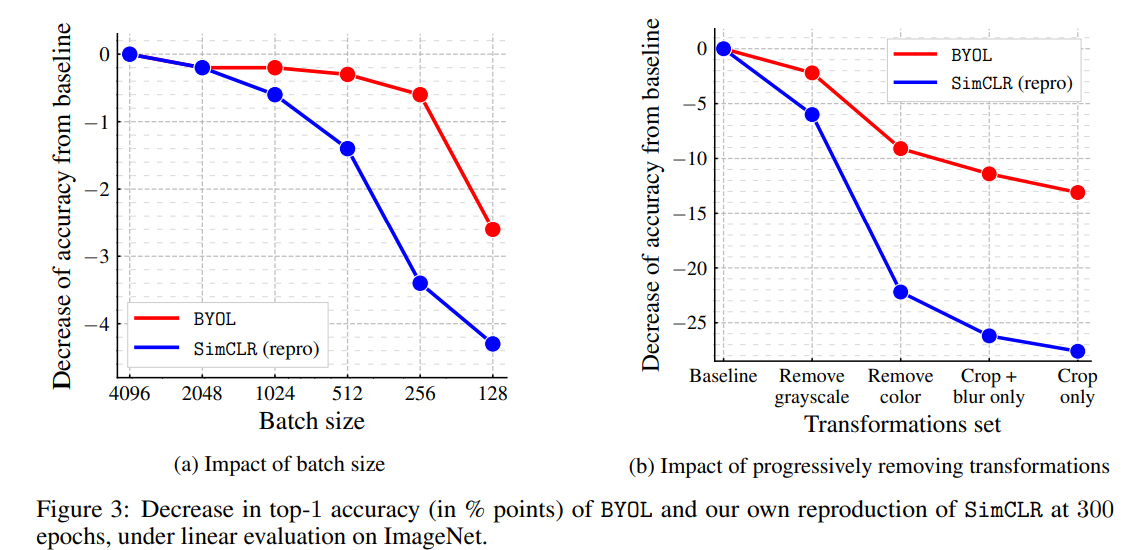
- 该方法性能最优,且
BYOL对batchsize和图像增强集合的变换相比其它方法更鲁棒。
本文的方法
自监督学习方法建立在跨视图的预测框架之上,即通过预测同一图像的不同视图来学习表示,该预测问题为一个图像的增强视图的表示应该预测同一幅图像的另一个增强图像的表示,但直接将预测问题投射到表示空间可能会导致崩溃解:即所有图像的不同视图的表示不变。对比方法规避这个预测问题,改为:从一个增强视图的表示中,学会区分同一图像的另一个增强视图的表示和不同图像的增强视图的表示。但是这种情况会需要比较每一个增强视图的表示与许多负样本的表示,文章则探讨了在防止崩溃解且保持高性能时,负样本是否必不可少。
为了防止崩溃解,一个直接的解决方案是使用一个固定的随机初始化的网络来产生需要预测的目标,在ImageNet上准确率达到,远高于随机初始化的网络本身,故BYOL的核心:从一个给定的特征(target),通过预测目标表征来训练一个新的、潜在增强的表征(online),在此基础上使用一个新的online网络作为下一次训练的新的target网络,在实践中,这里使用一个缓慢移动的online网络的指数平均作为target网络,而不是固定的checkpoints。
BYOL的描述
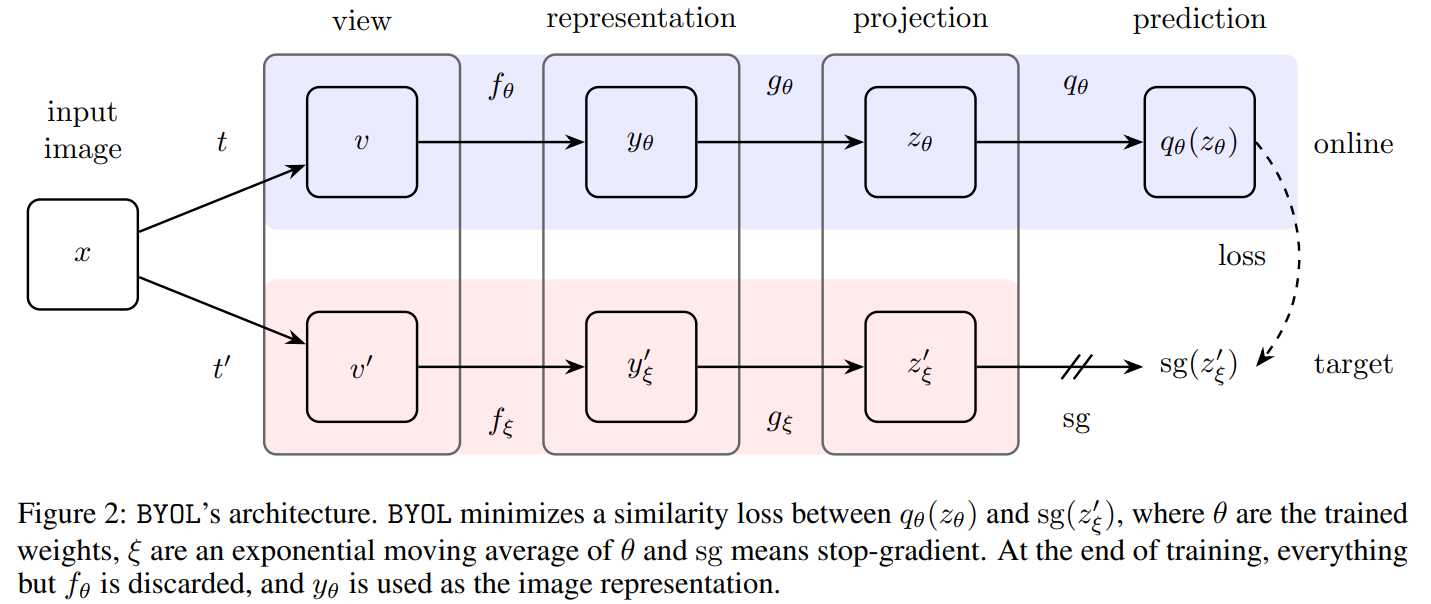
BYOL的目标是学习一种可用于下游任务的表征,如上图所示,BYOL包含两个神经网络:online和target网络。online网络权重为,由三个阶段组成:encoder、projector和predictor,target网络则权重为,目的是提供训练online网络的回归值,其参数由online网络的参数进行指数滑动平均,设,则:
给定图像集合和两个不同的图像增强分布和,采样一张图像,分别应用两个不同的图像增强方法,得到和。对于,online网络输出一个表征和一个投影;target网络则输出和目标投影;再输出的预测并分别做正则化,得到和,则采用均方误差,其损失如下:
对于对称损失,则额外将输入online网络,v输入target网络,计算损失,则总损失为,但反向传播每次只更新,这里称为stop-gradient,即:
其中是优化器的学习率,最后训练后,仅保留encoder。
算法如图:

损失函数与InfoNCE之间的关系
将SimCLR和BYOL的损失使用统一的形式,考虑如下的InfoNCE目标函数:
其中是固定的温度系数,是权重系数,是batchsize,和是来自一个batch的第个样本的增强视图,对增强视图之间的两两相似度进行量化,对任意的增强视图有,对于给定的和,使用归一化点积:
则对于SimCLR,其损失为(无predictor),(无target网络)和;对于BYOL,其损失为,且。
BYOL行为的直觉
BYOL通过只关于最小化,似乎BYOL应该收敛到对于最小的损失,即崩溃的常数表示,但的目标参数更新方向不是,故可防止崩溃解。假设BYOL的predictor是最优的,如:
假设这个不想要的平衡是不稳定的,在这个最优predictor的情况下,BYOL关于的更新基于期望条件方差的梯度:
其中是的第个特征。对于任意随机变量,有,其中为target投影,为当前的online投影,是在训练时online投影的随机变异性:单纯丢弃online投影中的信息不能降低条件方差。
特别地,BYOL避免的常数特性,对于任意的常数和随机变量,有,如果要关于最小化,则会得到崩溃解,相反BYOL使更接近,将online投影捕捉到的变异性整合到target投影中。
另外,如果直接将复制到也足以传播新的变化,但target网络突然的变化可能打破最优predictor的假设,此时损失不能接近条件方差,由此使用滑动平均并假设其主要作用是确保predictor在训练过程中接近最优性。
部分实验结果
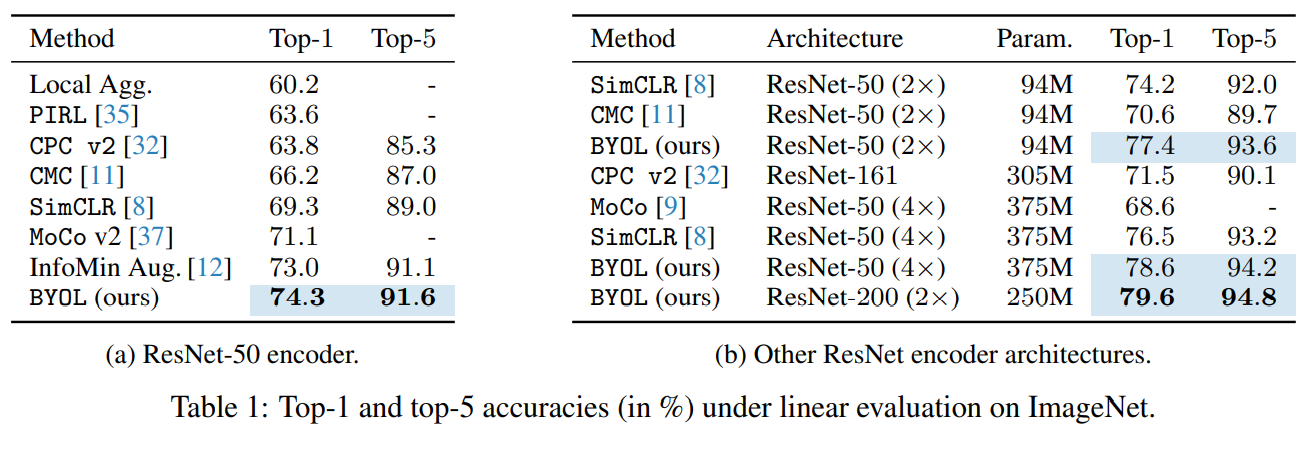
在ImageNet上的无监督结果:
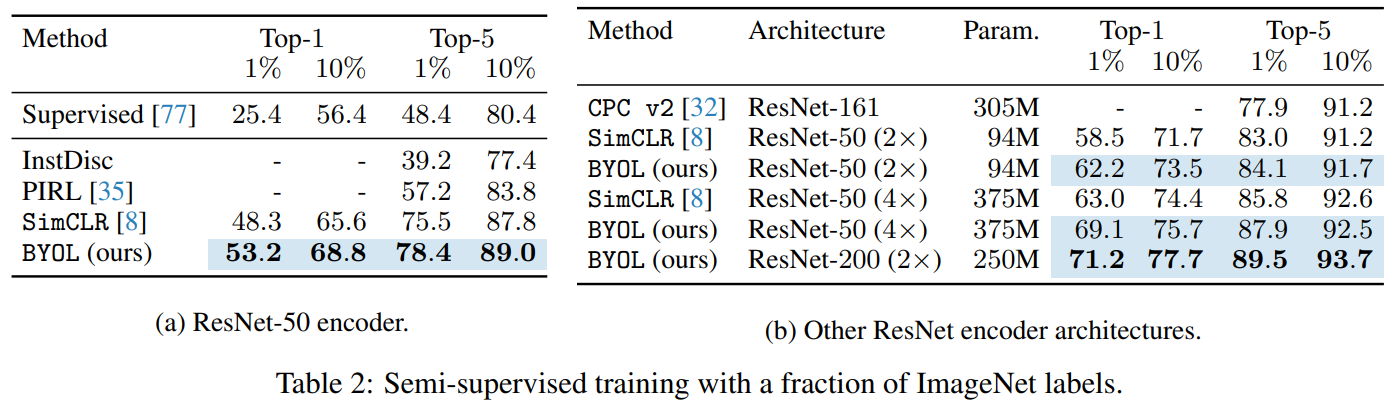
在ImageNet上的半监督结果:
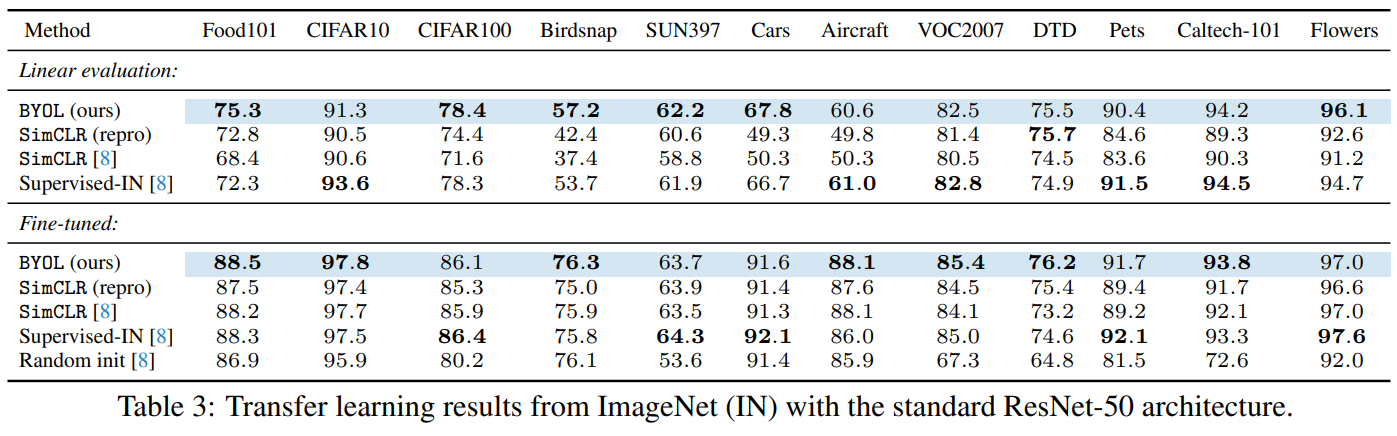
将ImageNet学习得到的特征迁移到下游任务:
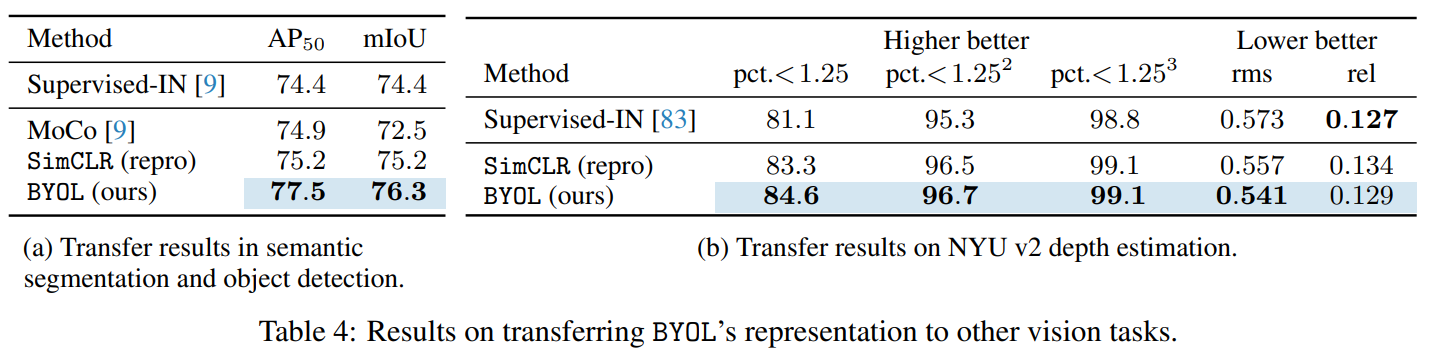
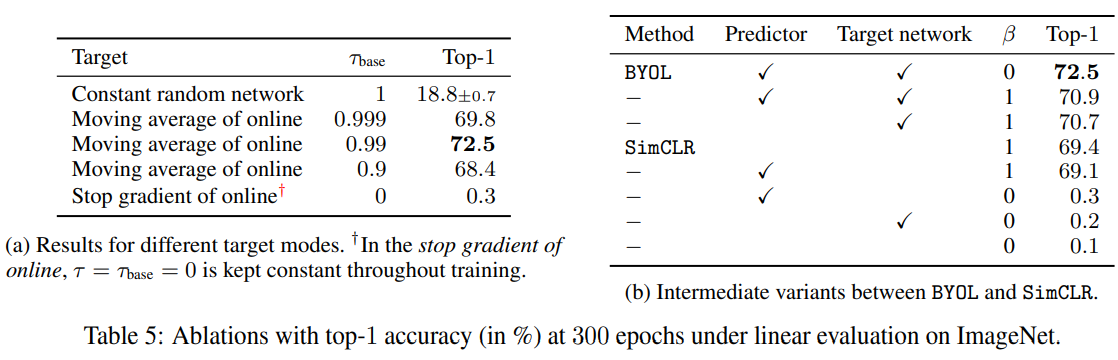
消融实验: