
动机
- 现有的对比学习方法依靠两两特征之间的显式比较,计算开销较大;
- 有证据表明在训练过程中比较更多的视图可以改进得到的模型,但大多数的对比方法对每幅图像只进行一对变换;
贡献
- 提出了一种新的在线聚类损失,即通过将图像特征映射到一组可训练的原型向量来避免对每一对图像进行比较,它对
batchsize的敏感度不高,且无需巨大的memory bank和momentum encoder;
- 提出了一种新的图像增强策略
multi-crop,简单地随机抽样不同分辨率的视图来代替两个全分辨率视图,带来性能上的提升且无额外的计算和内存开销。
本文的方法
本文提出了一种基于聚类的在线自监督方法,典型的基于聚类的方法是离线的,即在聚类分配步骤和训练步骤之间交替进行,前者是对整个数据集的图像特征进行聚类,后者是对不同图像视图预测的聚类分配,即codes。本文则不将codes作为目标,而只是加强同一图像的视图之间的映射的一致性,即可认为是比较多个图像视图之间的codes而不是特征。
即从图像的一个增强视图计算codes,而从其它增强视图上去预测codes。给定同一图像两种不同增强视图的特征和,通过将这些特征匹配到一组原型来计算对应的codes和,则设置为一个交换预测问题,损失如下:
其中是测量特征和code之间的契合度,即如下图所示,使用codes和来比较特征和,如果两个特征捕获了相同的信息,则从另一个特征预测codes也是可行的。
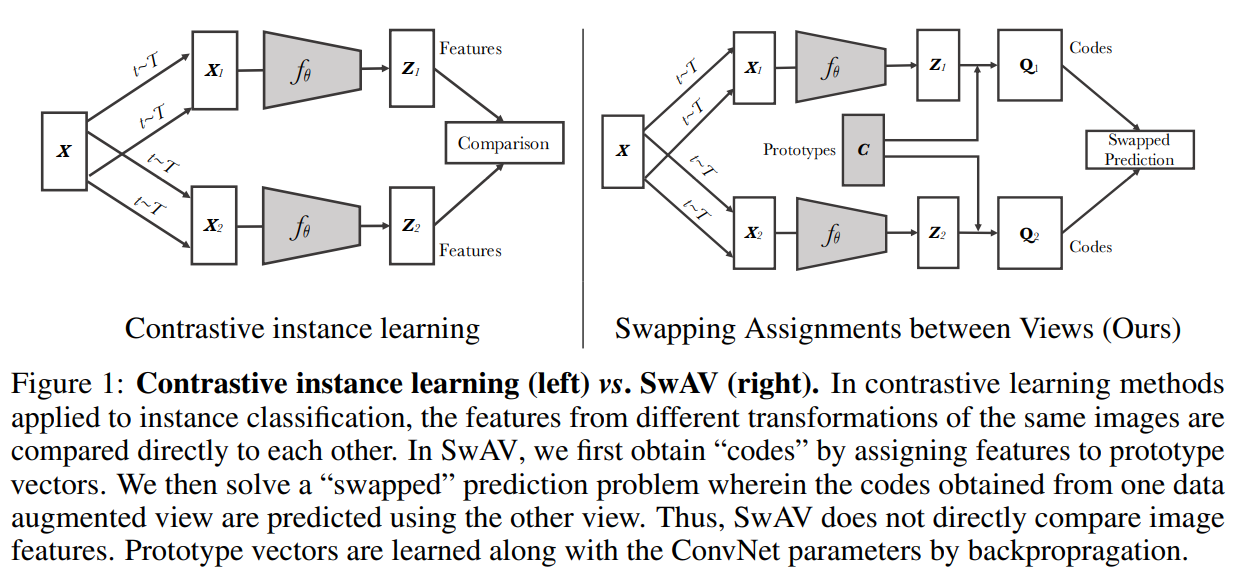
Online clustering
如上图,应用从图像变换集合中采样的变换,将每张图像变换为增强视图,通过应用非线性映射将增强视图映射到到向量表示,再投影到单位球面上得到,再映射到个可训练的原型向量来计算对应的code,用表示列为的矩阵。
交换预测问题
损失的每一项表示code和概率值的交叉熵损失,该概率由和中所有原型的点积经softmax得到,即:
对所有图像和数据增强对执行此损失,将得到如下的交换预测问题的损失函数:
通过最小化上述损失来联合优化原型和图像编码器。
在线计算code
参考博客:representation learning与clustering的结合(3): SwAV
使用原型来计算codes,使得在minibatch的所有实例都被原型等分,这种均分约束保证minibatch中不同图像的codes是不同的,从而防止出现每个图像都有相同的codes这种崩溃解情况。【补充:本来离线的聚类需要遍历整个数据集,而在线聚类只能在当前的batch中计算,故采用均分约束来防止崩溃解】给定个特征向量,去匹配原型和codes,通过优化去最大化特征和原型之间的相似度,即:
其中,为熵,为控制映射平滑度的参数,文中使用较小的,一个强的熵正则化可能导致崩溃解。【补充:假设的维度均为,则,,,则每个元素表示第个样本与第个聚类中心的相似度】作者参考以前的方法通过均分约束限制原型去使得在minibatch上有效:
其中表示维度为的向量,上述约束使得在batch中每个原型至少被选择次。
由于上式的解是连续值,【补充:可以将理解为标签,理解为预测值,一般来说标签采用one-hot的形式,本文验证连续值更好】如果通过四舍五入得到离散值对于小批量的在线学习效果较差,作者解释可能是变为离散值后收敛速度变快,优化过于激进,作者在实现时采用迭代以下公式求解:
其中和为重正则化向量,由Sinkhorn-Knopp算法迭代计算得到。
如果batchsize很小时,即当相对太小,不可能平均划分为个原型,则使用之前的batch中的特征来增大的大小,在计算训练损失时只使用当前batch特征的codes,实践中一般会存储的特征,远小于传统对比方法的。
Multi-crop
对于捕捉场景或目标的部分区域之间的关系信息,比较随机的图像crop发挥了重要作用,但增加crop或视图的数量会显著增加内存和计算需求,故作者使用两个正常分辨率的crop和采样个低分辨率的部分图像信息的crop:
在这里,只使用标准分辨率的crop来计算codes,为所有crop计算codes会增加计算时间且影响网络性能(可能是由于部分图像信息会降低特征到codes的映射能力)。
部分实验结果
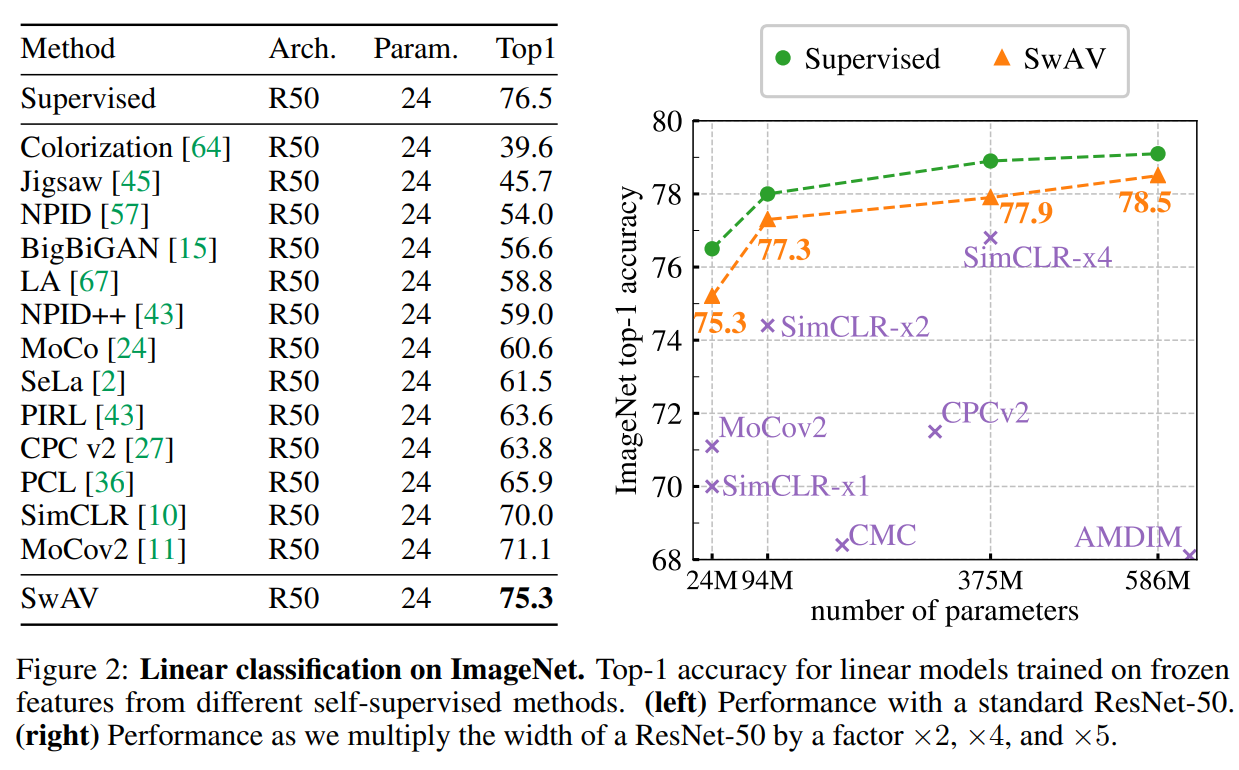
无监督学习在imagenet的表现:
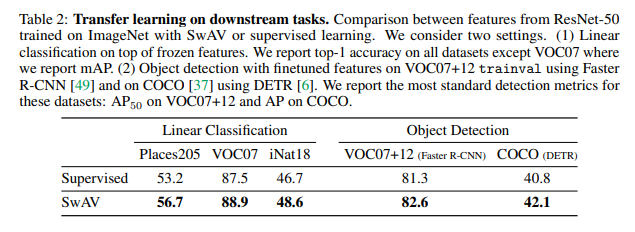
将无监督学习得到的特征迁移到下游任务:
小批量的训练:





