动机
- 现有的领域自适应的目标重识别方法通常采用基于聚类的伪标签方法,该方法由于域间的差异和聚类性能不佳,没有充分利用所有有价值的信息;
- 一是在目标域微调的过程中,要么忽略了源域数据(仅用于预训练),要么由于方法设计的局限性,会对性能造成损害;
- 二是在聚类过程中可能产生离群值,现有的方法通常将离群值丢弃而不用于训练,但这些离群值可能是目标域中困难但有价值的样本,而在训练早期通常有大量离群值,若简单地丢弃会损害最终性能。

贡献
- 提出了一个统一的对比学习框架,将源域和目标域的所有可用信息纳入到联合特征学习中,并利用混合记忆模型
Hybrid Memory来提供三种监督:class-level、cluster-level、instance-level(分别对应源域、目标域聚类、目标域离群值);
- 设计了一种新的带有聚类可靠性准则的自步对比学习策略,以防止伪标签噪声导致的训练误差被放大,它逐渐生成更可靠的目标域聚类,用于在混合记忆模型中学习更好的特征,进而提高聚类能力。
领域自适应的目标重识别
目的是将学习到的知识从有标注的源域数据转移到无标注的目标域数据,解决开放类的重识别问题,一般认为重识别任务上的两个域之间的类别完全没有重复。
现有的方法主要分为两类:基于伪标签的方法和基于域转换的方法,作者发现伪标签能更有效地捕捉目标域分布,故文章采用基于伪标签的方法,一般来说该方法采用两阶段的训练方案:1)在有标注的源域进行预训练;2)适应带有伪标签的目标域。而伪标签可以通过聚类实例特征或测量与范例特征的相似性来生成,文章采用聚类生成伪标签。训练时在通过聚类目标域的实例生成伪标签和用生成的伪标签训练网络之间交替进行,由此源域预训练的网络就可以适应在伪标签有噪声的情况下捕获目标域的样本间关系。
基于聚类的方法面临的主要挑战是如何提高伪标签的精度以及如何减轻伪标签噪声带来的影响。
本文的方法
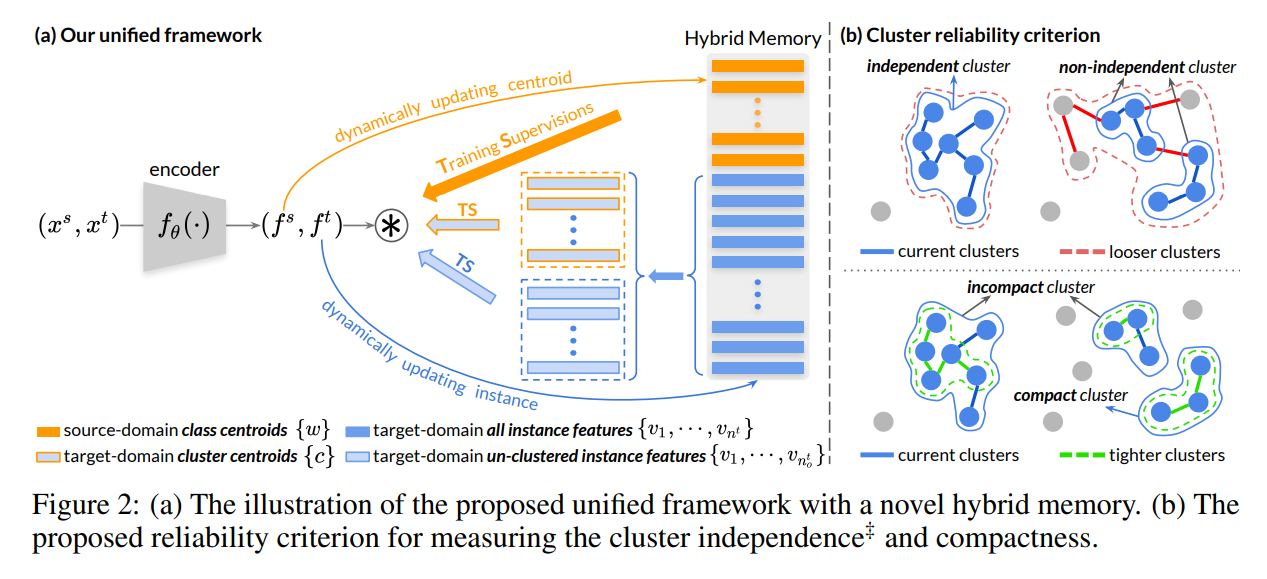
本文的网络框架如上图(a),由源域class-level、目标域cluster-level和目标域un-clustered instance-level三种监督共同训练编码器,并在hybrid memory中动态更新以逐步提供更可靠的学习目标。为了避免聚类噪声导致训练误差增大,首先选择最可靠的聚类进行初始化,并引入一种新的可靠性准则来评估聚类的质量,由此逐步纳入更多的未聚类的实例,形成新的可靠的聚类。故训练过程为以下两个步骤之间交替进行:1)将目标域样本通过带自步学习策略的hybrid memory中的目标域实例特征聚类分组为cluster和un-clustered instances;2)使用对比损失更新编码器并动态更新hybrid memory中的编码特征。
使用对比学习构建和更新Hybrid Memory
对于无标签的目标域的训练样本,采用自步聚类策略分组为cluster和un-clustered outlier,由此所有的训练集可用被分为三个部分:带有真实标签的源域样本、带有伪标签的簇类目标域数据和不属于任何簇类的目标域实例,即,以往的方法只使用目标域簇类数据,而本文则设计了一种新的对比损失利用所有可用数据:
统一对比学习
给定一个特征向量,本文的对比损失如下:
其中是对应的正类原型,表示两个特征向量的内积以计算相似度,是源域类的数量,是目标域簇的数量,而是目标域非簇的实例数量。对于正类原型的选择,如果为源域特征,则是所属的源域真实类别所对应的质心;如果为目标域簇内的样本特征,则是第个簇类的质心;如果为目标域聚类离群值,则是该离群点对应的实例特征。直观上希望编码后的特征向量向其指定的类、簇或实例靠拢,且使用类中心而不是可学习的权重来编码源域类,以使得在语义上跟目标域的中心匹配,否则语义不匹配会导致性能显著下降。
Hybrid Memory
由于交替的聚类策略,在训练过程中,簇类数和离群点实例数可能发生变化,因此,统一对比损失的类原型采用非参数动态构建。
初始化
利用提取的特征对hybrid memory进行初始化,对于源域则计算每个类的平均特征向量作为初始源域类中心,初始目标域实例特征则由编码得到,再用各簇的平均特征向量初始化目标域的聚类中心,即。
更新
对于源域类中心,第个质心用mini-batch中属于类的编码特征的均值更新:
其中,表示当前mini-batch中属于源域类别的特征集合,是一个动量系数。
对于目标域簇中心,不能以与源域类中心相同的方式存储和更新,因为和在不断的变化。由于hybrid memory缓存了所有目标域特征,则利用mini-batch中每个已编码的特征向量更新其对应的实例:
对于更新后的实例存储,如果属于簇,则需要用更新相应的质心。
具有可靠聚类的自步学习
由于本文将目标域的簇类和未聚类的离群点视为不同的类,故聚类的可靠性会显著影响到学习的表征。实践中发现将一个实例合并到一个错误的簇类会弊大于利,故引入自步学习的策略,在每次epoch重新聚类的步骤前,只保留最可靠的聚类结果,不可靠的聚类结果则拆回成未聚类的实例。文章提出了一种新的可靠性准则,通过测量簇的独立性和紧凑性。
聚类的独立性
一个可靠的聚类应该独立于其它簇和单个样本,即如果一个聚类与其它样本的距离较远,则可认为是高度独立的,定义具有相同簇类的的样本为,利用IOU来评估独立性:
其中,表示聚类准则变松弛时包含的的聚类集合,越大则表明具有更独立的聚类,同一个聚类集合的样本应该具有相同的独立性分数。
聚类的紧凑性
一个可靠的聚类也应是紧凑的,即同一个类之间的样本有一个小的类内距离,即使给定更严格的聚类准则,也不会被分割,紧凑性定义如下:
其中,表示聚类准则变紧时包含的的聚类集合,越大则表明具有更小的类间距离,因为当采用更严格的准则时,样本间距离较大的聚类更可能包含较少的点。由于密度的不均匀,同一簇的数据点可能具有不同的紧凑性分数。
由以上指标,计算聚类结果中每个数据点的独立性和紧凑性得分,并设置相应的阈值来获取可靠的聚类结果,即保留具有紧凑数据点的独立簇,即且,剩余数据被视为未聚类的离群点,随着hybrid memory对编码器的更新和目标域实例特征的更新,逐步创建更可靠的簇,进一步提高表征学习。
部分实验结果
域适应的行人重识别实验结果:
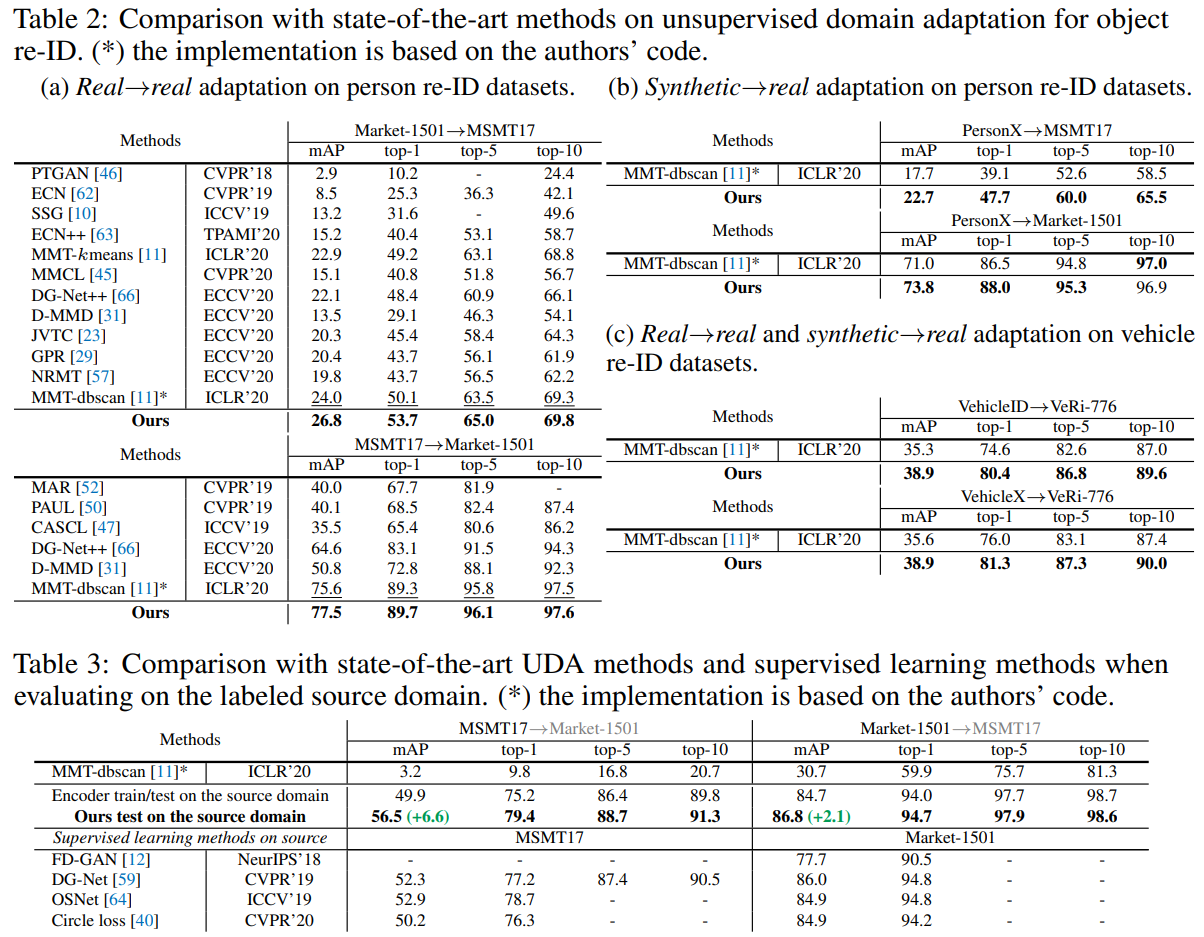
无监督的行人重识别实验结果:
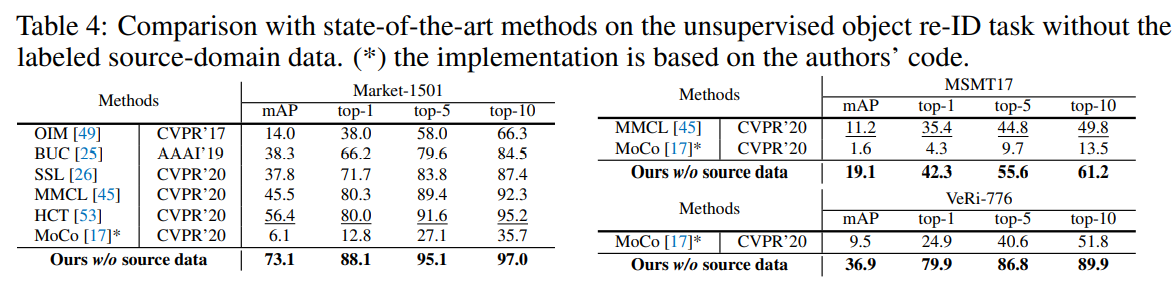
消融实验: