动机
- 孪生网络是无监督/自监督表征学习模型中常见的结构,最近方法的输入为一个图像的两个增强图像,在不同的条件下最大化两个增强图像之间的相似性以避免崩溃解;
- 孪生网络的一个不希望的解决方案是所有输出崩溃为一个常数,
SimCLR通过对比学习的思想,拉近正对排斥负对,负对排除了解空间中的常量输出;SwAV将online clustering整合到孪生网络中;BYOL则在使用动量编码器的条件下只依赖正对。
贡献
- 通过实验结果表明,即使不使用1)
negative sample pairs; 2)large batches; 3)momentum encoders,孪生网络也可以学到有意义的表征,即直接最大化一个图像的两个视图的相似性,既不使用负对也不使用动量编码器; - 通过实验证明,对于损失和结构而言,存在崩溃解问题,但是
stop-gradient操作在防止崩溃解中发挥了关键的作用; - 证明了由于孪生网络具有的建模不变性的特征,是目前的表达学习方法成功的关键原因所在,这也是表达学习的核心所在。
本文的方法
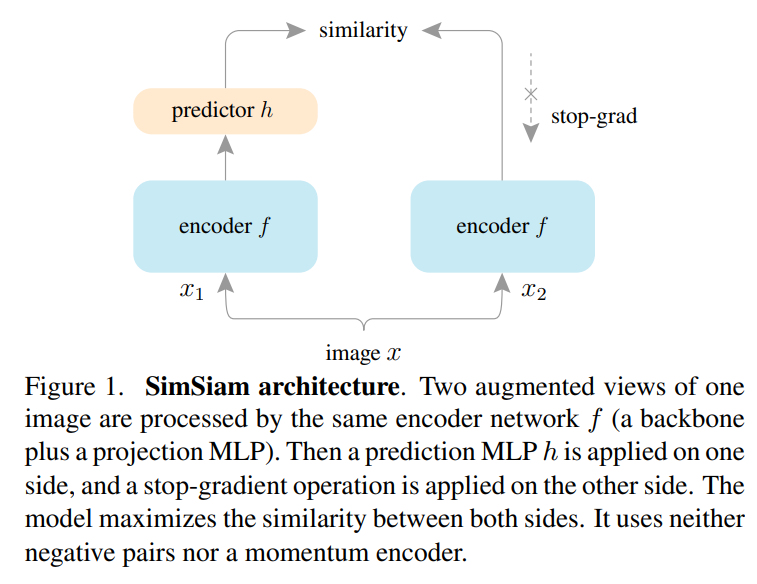
上图为本文的网络框架,输入是图像的两个随机增强视图和,两个视图通过相同的编码器提取特征并映射到高维空间,此外一个预测模块将其中一个视图转换并于另一个视图匹配,该过程为和,则损失函数为最小化负余弦相似度:
其中为归一化,等价于归一化向量的均方误差,此外结合stop-gradient操作定义了一个对称损失,则:
即对于第一项,不会从接收梯度信息,但在第二项会从接收梯度信息,则相反,下图是对应的伪码:

与其它方法的关系
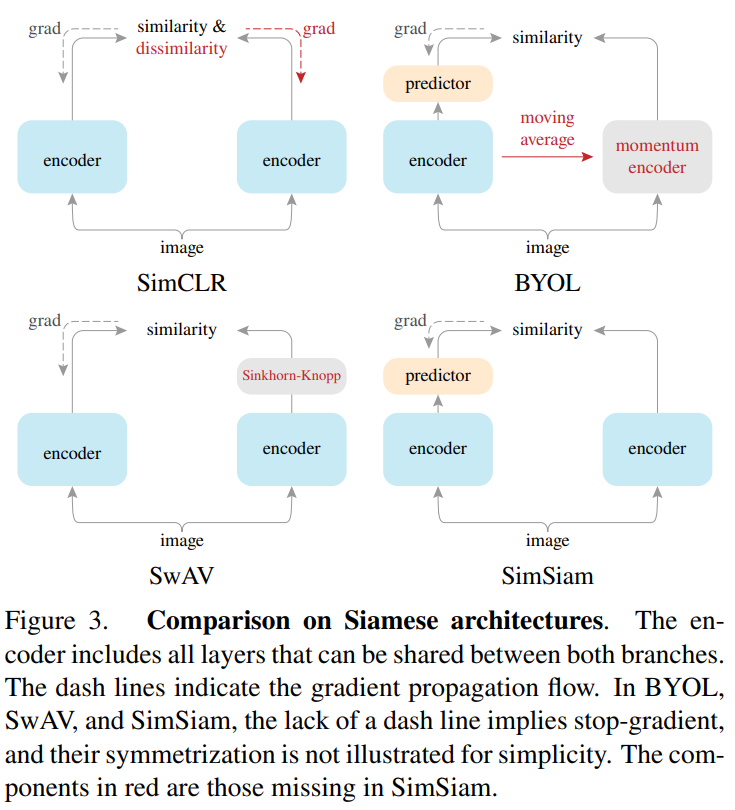
SimSiam可以作为一个中心来关联几个现有的方法:SimCLR依赖于负采样以避免崩溃解,SimSiam可以看作是SimCLR without negative;SwAV通过在线聚类来避免崩溃解,SimSiam可以看作是SwAV without online clustering;BYOL使用动量编码器,SimSiam可以看作是BYOL without the momentum encoder。
实证研究
本节从实验方面去验证什么行为有助于模型得到非崩溃解?
Stop-gradient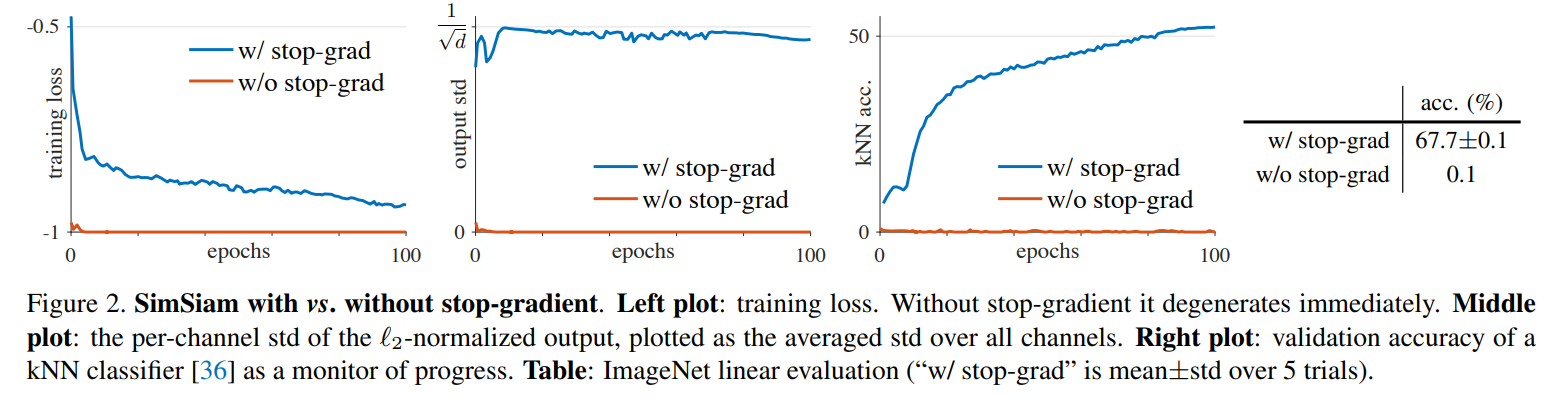
通过上图可知,无
stop-gradient的时候其损失会迅速到达可能的最小值,且其输出的归一化的标准差为,并且分类结果很差。Predictor
如果没有
predictor,则损失为,此时等价于不使用stop-gradient并加上缩放系数,故仍会崩溃;如果predictor在训练时固定,则训练不会收敛。Batch Size
由上图可知,从小
batch size到大batch size,方法均有效。Batch Normalization
由上图可知,
BN有助于训练优化,但并未看到BN有助于防止崩溃的证据。Similarity Function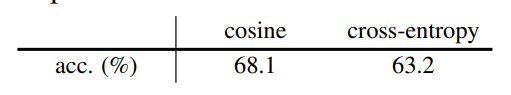
由上图可知,对于交叉熵相似度,即损失为,该方法也是有效的。
Symmetrization
由上图可知,非崩溃解不依赖于对称损失,但对称损失有助于提升精度。
由上述实验得知,对于避免崩溃起关键作用的是stop-gradient操作。
假设
本节从理论方面去讨论本文的方法SimSiam在隐式地优化什么?
文章的假设是SimSiam是一个类似于期望最大化(EM)算法的实现。它隐式地涉及到两组变量,并解决两个潜在子问题,stop-gradient的出现是引入额外的一组变量的结果,损失如下:
其中,是特征提取网络,是增强方法,是图像,额外引入一个,它是的表示,下标表示使用图像索引访问图像的子向量,其大小正比于图像数量。所以优化问题如下:
描述形式如同k-means,是编码器可学习的参数,类似于聚类中心,是的表征,类似于样本的对应向量(如k-means的one-hot向量),由此通过交替求解两个子问题:
对于的求解,使用SGD进行求解,由于被固定,故stop-gradient是一个很自然的操作;对于的求解,通过如下的式子:
所以SimSiam可以认为是上述两个子问题的一次交替的近似。
上述分析并不包含预测器,且上述分析并不包含对称损失,对称损失并非该方法的必选项,但有助于提升精度。
并且文章通过实验得到多步的交替优化更新也是有效的:
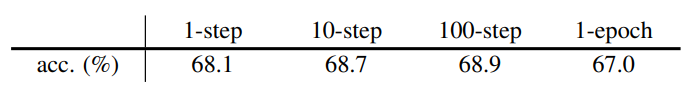
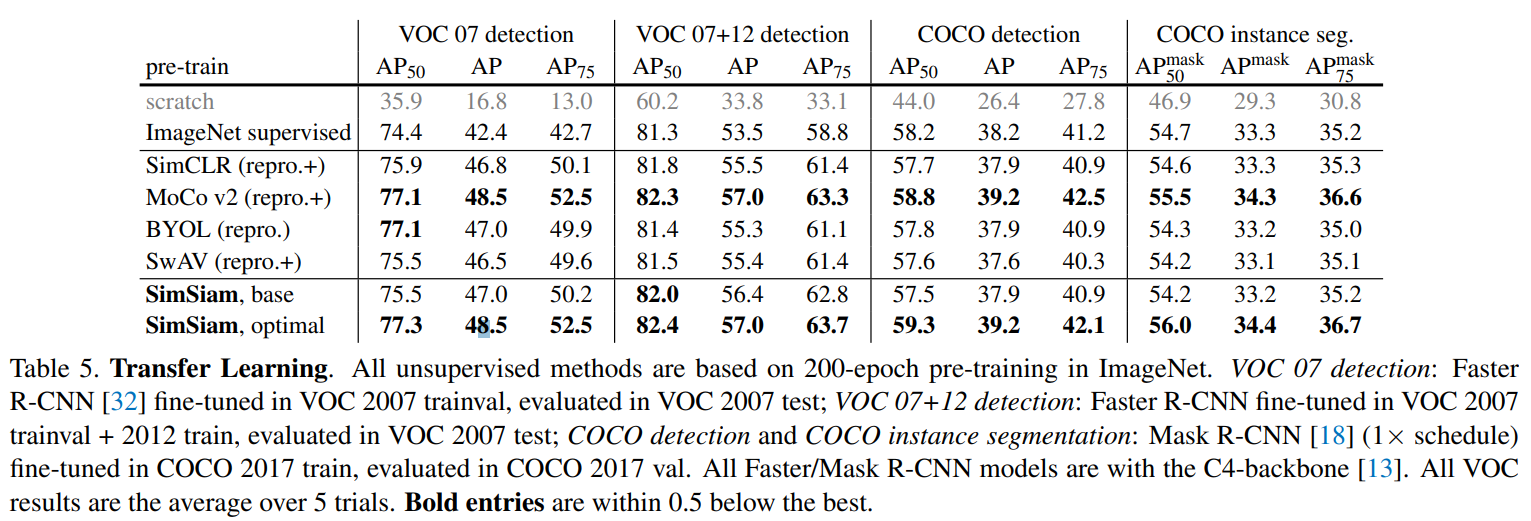
部分实验结果
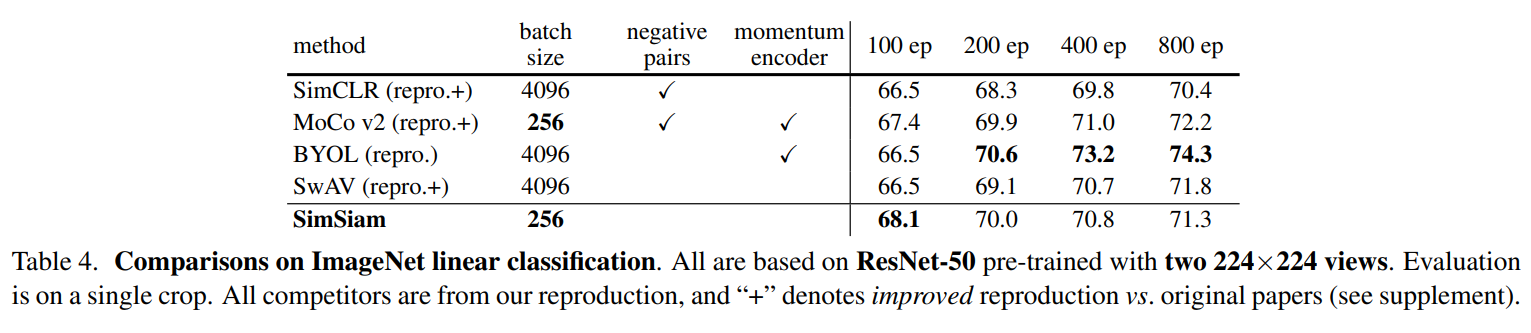
在ImageNet上的分类准确率结果:
迁移学习的结果: