You got a dream, you gotta protect it.

0%

论文阅读-disentanglement-InfoGAN-CR and ModelCentrality_Self-supervised Model Training and Selection for Disentangling GANs

发表于 分类于 Valine： 本文字数： 3.6k 阅读时长 ≈ 3 分钟
InfoGAN-CR与模型中心性:自监督模型训练与选择的解纠缠GAN-ICML2020

动机

  • 设计解纠缠生成模型时，存在两个主要障碍：设计具有良好解纠缠性和良好样本质量的架构，和给定一个固定的架构，进行超参数调整和模型选择；
  • 对于第一个问题，VAE的方法(如beta-vae、factor-vae)主要通过正则化总相关性来促进不相关性，以牺牲图像质量来获取更好的解纠缠分数，而GAN的方法(如infogan)通过增加隐编码的输入，并对损失函数增加一个额外的正则化来促进信息性，尽管样本质量更好，但解纠缠分数较低，这导致在GAN网络上的解纠缠进展较慢；
  • 对于第二个问题，当前超参数调优的常见做法是通过交叉验证标记了真实潜在编码的数据集，即样本用已知的解纠缠的隐编码进行标记，这极大的限制了对于真实数据集未知标签的有效性。

贡献

  • 设计了一种新的解纠缠的GAN的架构InfoGAN-CR，它增加了一个对比正则化器，它结合了自监督和解纠缠的自然方法：潜在遍历；
  • 引入了一种新的基于自监督的模型选择方法ModelCentrality，它基于一个假设：良好解纠缠的模型是相近的，其相近程度由一种解纠缠度量方法来度量。文章对这个假设进行数值验证并将ModelCentrality定义为在这个解纠缠度量下的一系列模型的多维概化，它根据与其它模型的相近程度定义自监督标签，为每个模型分配相应的分数；
  • 实验证明比目前的VAE和GAN方法，文章在不使用监督数据的情况下显著提升了解纠缠的分数。

本文的方法

自监督的对比正则化

一种判断解纠缠的自然方法：在隐编码上做潜在遍历的实验，将鼓励模型生成图像做出明显的改变。

在此基础上，设计一个Contrastive Regularizer(CR)，即固定相同的一个隐编码 c_i ，其它隐编码通过均匀随机采样，由此生成多张图像，让 (x,x’) \sim Q^{(i)} 表示因子 c_i 固定时的样本对分布。并使用 JS 散度来衡量这种潜在遍历的显著性：

d_{\mathrm{JS}}\left(Q^{(1)}, \ldots, Q^{(k)}\right) \triangleq \frac{1}{k} \sum_{i \in \mid k]} d_{\mathrm{KL}}\left(Q^{(i)} \| \bar{Q}\right)

其中 \bar{Q}=(1 / k) \sum_{j \in[k]} Q^{(j)} ，上式用来测量每个隐编码遍历的差异性，若最大化上式作为生成器训练的正则化器，则生成器会迫使 Q(i) 变得尽可能不同，反过来又迫使隐编码中的变化使图像发生明显的变化，并且容易与其它隐编码的变化区分开。

网络结构

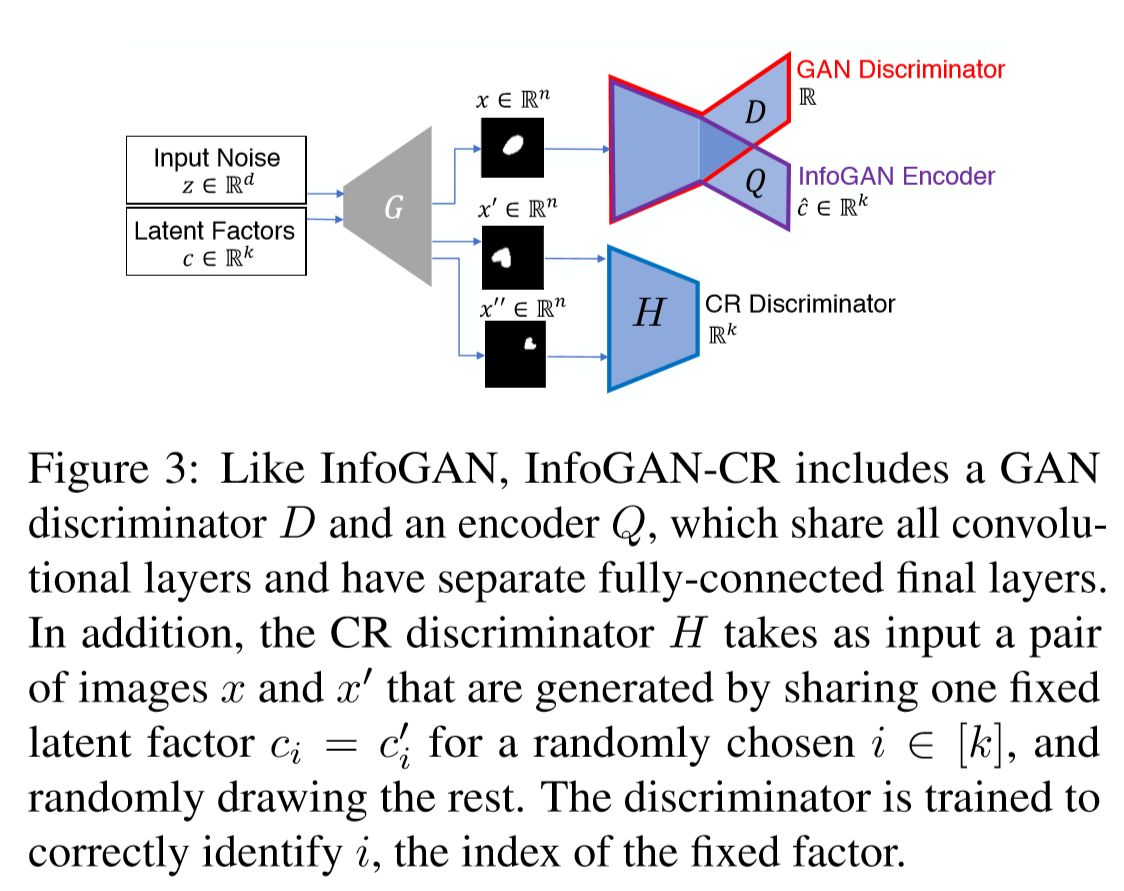
为了近似上文提出的对比正则化器，引入一个额外的判别器 H:\mathbb{R}^n \times \mathbb{R}^n \rightarrow \mathbb{R}^k 来执行多路假设检验，由此得到新的损失函数：

\min _{G, H, Q} \max _{D} \mathcal{L}_{\mathrm{Adv}}(G, D)-\lambda \mathcal{L}_{\mathrm{Info}}(G, Q)-\alpha \mathcal{L}_{\mathrm{c}}(G, H)

图像对 x 和 x’ 是根据隐空间遍历的定义生成的，判别器 H 目标是希望判别出在图像对之间共享的编码，生成器和判别器都希望 k 路假设检验成功，文章使用标准的交叉熵损失：

\mathcal{L}_{\mathrm{c}}(G, H)=\mathbb{E}_{I \sim \mathrm{U}([k]),\left(x, x^{\prime}\right) \sim Q^{(I)}}\left[\left\langle I, \log H\left(x, x^{\prime}\right)\right\rangle\right]

其中 Q^{(I)} 表示图像对的联合分布， I 是随机索引的onehot编码， H 是一个输出为 k 维向量的神经网络，对于所有的 x 和 x’ ，输出被归一化为 \left\langle\mathbb{1’}, H\left(x, x^{\prime}\right)\right\rangle=1 ，这会鼓励每个潜在代码进行明显的更改，从而促进解纠缠。

渐进式训练

即在训练过程中逐步改变假设，使得网络由易到难训练。首先在 k 个索引中选择一个随机索引 I ，并从选择的隐编码 c_I\in \mathbb{R} 中采样，由此生成两张具有相同 c_I 的图像，而剩下的因子被独立随机选择。令 c_j^m 表示图片 m\in\{1,2\} 的第 j 个隐编码，contrastive gap被定义为 \min _{j \in[k] \backslash\{I\}}\left|c_{j}^{1}-c_{j}^{2}\right| ，这个gap越大则表明图像对之间的显著性越大，在训练时逐步减小这个gap。

模型中心性:自监督的模型选择

之前的方法是有监督的，其性能评估要求能够访问真实解纠缠编码的生成数据，有监督的超参数调整存在两点问题：现实应用时可能不存在真实标签数据；对于更复杂的模型，可以通过充分的搜索去得到更好的分数。

模型中心性

假设想从数据中发现一个最优解纠缠，则良好的解纠缠模型应该接近最优模型，即各个良好的解纠缠模型应该彼此接近，之前的工作表明良好解纠缠的模型趋向于表现出质量上好的解纠缠属性，这表明解纠缠分数可以衡量一个模型解开的隐编码和另一个模型解开的隐编码之间的距离。

考虑一个训练模型 G:\mathbb{R}^k\rightarrow\mathbb{R}^n 将解纠缠的隐编码映射到图像，现有的度量方法需要相应的编码器 Q:\mathbb{R}^n\rightarrow\mathbb{R}^k ，它将样本映射到估计的解纠缠隐编码，原始的FactorVAE score要求使用具有真实隐编码的训练数据的监督，本文则使用一个训练模型作为真实标签的替代，即模型中心性将另一个模型 G_j 的分布作为真实标签。给定两个训练模型 G_i 和 G_j ，能够测量编码器 Q_i 估计从模型 G_j 的生成样本中学到的隐编码，由此计算 G_i 和 G_j 之间的相似性：1)由目标模型 G_j 生成图像，2)将这些样本通过模型 G_i 的 Q_i 去预测隐编码，3)以目标模型 G_j 生成的隐编码作为真实标签，由此评测FactorVAE score。

给定 N 个经过训练的生成模型，以模型 G_j 为目标模型，按照上述方法计算模型 G_i 的解纠缠得分。然后定义对称相似度矩阵 B∈\mathbb{R}^{N×N} ，其中 B_{ij}= (1/2)(A_{ij} + A_{ji}) 表示模型 i 与模型 j 的相似度，本文选择FactorVAE score作为解纠缠度量。

部分实验结果

定量对比和定性实验

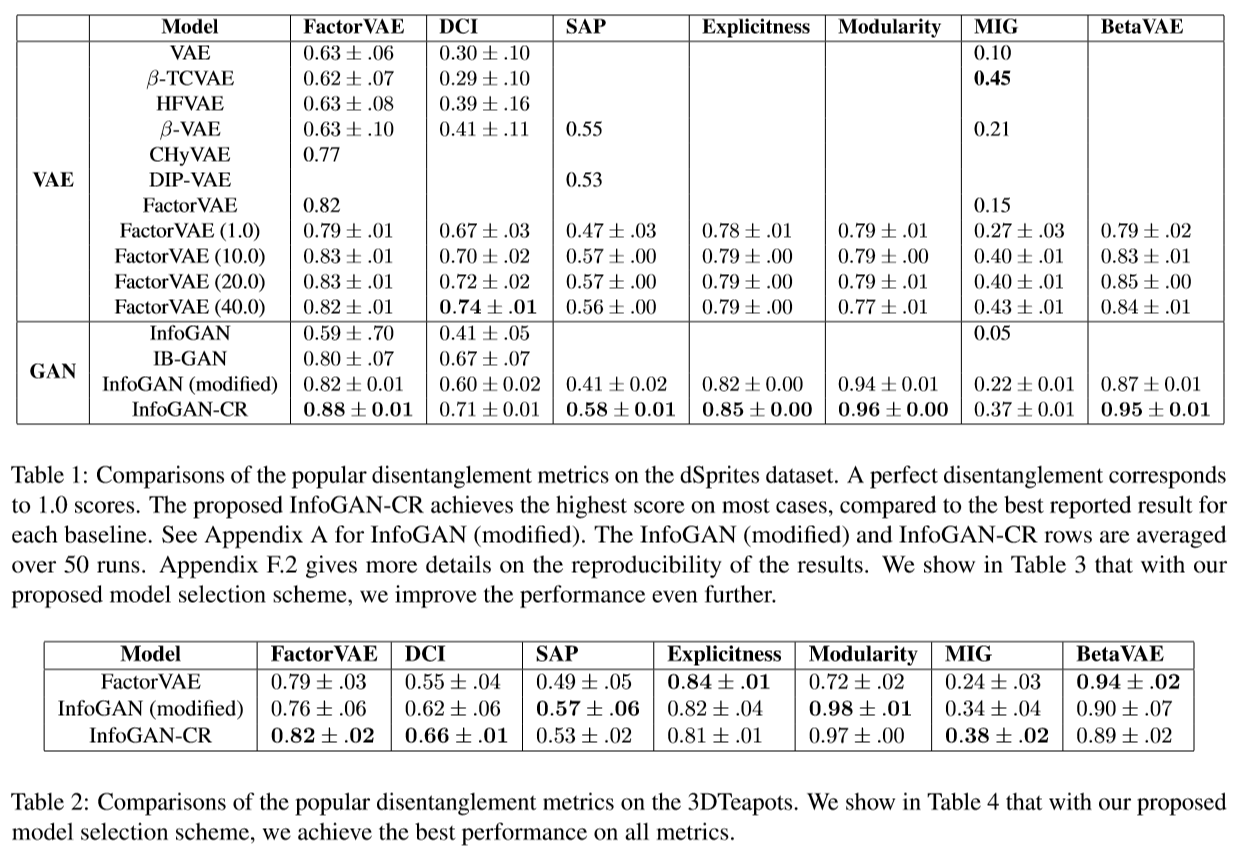
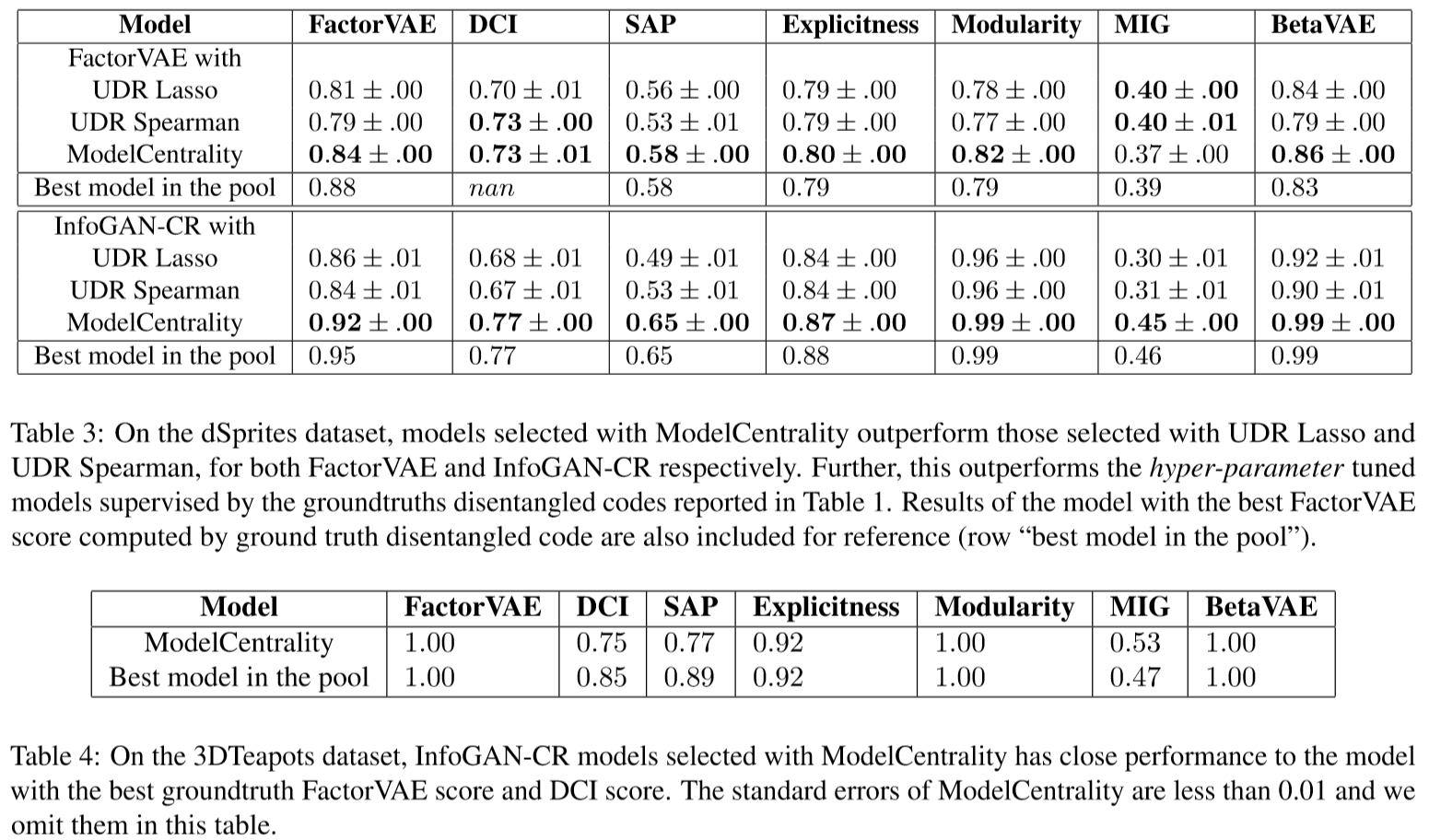
采用模型中心性选择的模型的实验

相关文章