You got a dream, you gotta protect it.

0%

深度学习-连续的解纠缠评测方法(基于各种VAE)

发表于 更新于 分类于 Valine： 本文字数： 9.2k 阅读时长 ≈ 8 分钟
连续的解纠缠评测方法(基于各种VAE)

2020-10-14 update beta-VAE metric, factor-VAE metric, MIG, SAP Score, DCI

2020-12-22 update Modularity，Locatello论文方法设置

本文是基于Challenging Common Assumptions in the Unsupervised Learning of Disentangled Representations的论文和NeurIPS2019 Disentanglement Challenge对连续的解纠缠方法的度量方法，主要对相应的评测方法的原理进行简单讲解，文章分别提到了beta-VAE metric、factor-VAE metric、MIG、SAP Score、DCI、Modularity和IRS。

beta-VAE metric

原文：beta-VAE: Learning Basic Visual Concepts with a Constrained Variational Framework

方法

将某个变化因子固定而其余的因子随机变化，由此生成 L 对的数据 x 和 x’ ，再得到对应的表征 z 和 z’ (定义为 q(z|x) 的均值)，计算每对 z 和 z’ 之间差的绝对值，再将这些统计量的平均值作为线性分类器的输入，固定因子 k 为对应的输出，理想状态下如果表征被完全解耦，则在输入的维度上对应的固定的变化因子的维度为0，分类器就会学会将零值的维度索引映射到固定变化因子的索引上。

缺点

  • 对线性分类器优化的超参数敏感；
  • 使用线性分类器不那么直观，即会得到每个因子对应维数的线性组合而不是单一维数的表示；
  • 即使 K 个变化因子中只有 K-1 个变化因子被解纠缠，依然为 100\% 的准确率(见factor_vae)。

Factor-VAE metric

原文：Disentangling by Factorising

方法

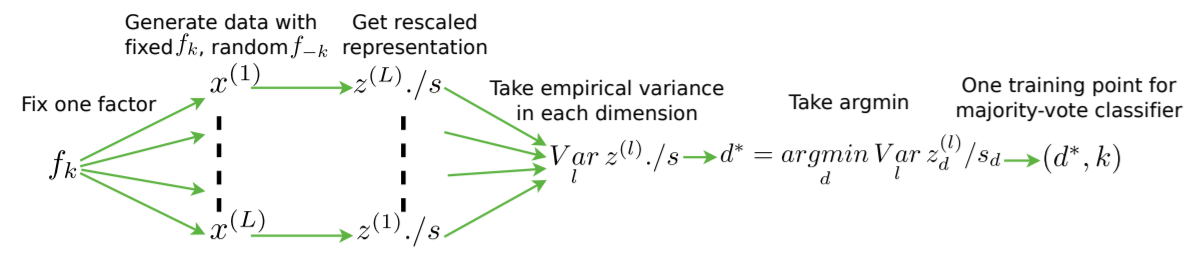
选择某个变化因子 k ，生成该因子固定而其余的因子随机变化的数据，由此得到L个数据 x ，再得到对应的表征 z ，并通过足够大的数据集对 z 的各个维度使用经验标准差进行归一化处理，然后对这些标准化表示在每个维度计算方差，方差最小的那个维度的索引则对应于固定的因子 k ，即分类器的输入和输出。所以理想情况下，如果完全解纠缠，则固定的变化因子对应的维度上的经验方差应该为0，由于输入和输出均位于离散空间，这里分类的方法是使用投票法，无超参数，但依然是有监督的方法。

MIG(Mutual Information Gap)

原文：Isolating Sources of Disentanglement in Variational Autoencoders

方法

假设真实因子 p(v_k) 和生成过程 p(n|v_k) 已知且可被(如经验分布)量化，且对于所有的 j ， q(z_j|n) 是已知的且可以采样的；那么对于任意的 q(z|n) ，文章认为隐变量 z_j 和真实因子 v_k 之间的互信息可以用联合分布 q\left(z_{j}, v_{k}\right)=\sum_{n=1}^{N} p\left(v_{k}\right) p\left(n \mid v_{k}\right) q\left(z_{j} \mid n\right) 表示，则互信息为：

I_{n}\left(z_{j} ; v_{k}\right)=\mathbb{E}_{q\left(z_{j}, v_{k}\right)}\left[\log \sum_{n \in \mathcal{X}_{v_{k}}} q\left(z_{j} \mid n\right) p\left(n \mid v_{k}\right)\right]+H\left(z_{j}\right)

其中 H(z_j) 是隐变量 z_j 的熵， \mathcal{X}_{v_{k}} 是满足 p(n|v_k) 的样本集合，期望是通过显式地采样来实现的。

可以看出，更高的互信息表示 z_j 包含 v_k 中的更多的信息，即如果 z_j 和 v_j 存在确定的互逆关系，则互信息应该最大，对于离散的 v_k ，有 0\le I(z_j;v_k)\le H(v_k) ，其中 H\left(v_{k}\right)=\mathbb{E}_{p\left(v_{k}\right)}\left[-\log p\left(v_{k}\right)\right] 是 v_k 的熵。虽然可以通过直接计算平均的最大 MI 来作为度量方法，即 \frac{1}{K} \sum_{k=1}^{K} \frac{I_{n}\left(z_{k^{*}} ; v_{k}\right)}{H\left(v_{k}\right)} ，但这样可能会出现一种情况，即一个因子 v_k ，可能与多个 z_j 有很高的互信息，通过计算具有最高的互信息的前两个隐变量之间的差异来强制轴对齐，故使用下式：

\frac{1}{K} \sum_{k=1}^{K} \frac{1}{H\left(v_{k}\right)}\left(I_{n}\left(z_{j^{(k)}} ; v_{k}\right)-\max _{j \neq j^{(k)}} I_{n}\left(z_{j} ; v_{k}\right)\right)

其中 j^{(k)}=\operatorname{argmax}_{j}\ I_{n}\left(z_{j} ; v_{k}\right) ， K 是已知的因子的数目，MIG的值为[0,1]的区间，作者认为这种方法的优点就是轴对齐的且无偏的，就是一个潜变量 z_j 只和一个真实的 v_k 相关。上式能够防止两种重要的情况：第一种情况与因子的旋转有关，当一组潜在变量不是轴对齐的时候，每个变量可以包含关于两个或更多因子的信息，这个差值会惩罚未对齐的变量；第二种情况与表示的紧密度有关，即如果一个潜在变量可靠地模拟了一个真实的变化因子，那么其他潜在变量也不必关联这个因子了。

SAP(Separated Attribute Predictability) score

原文：Variational Inference of Disentangled Latent Concepts from Unlabeled Observations

方法

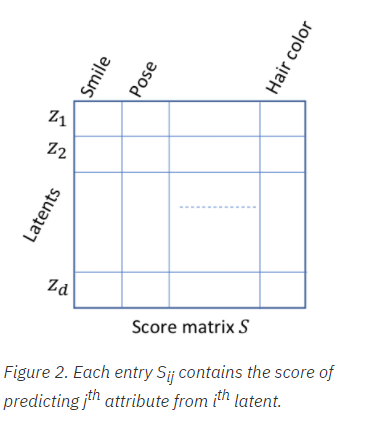
首先创建一个 d\times k​ 的分数矩阵 S​ ，其中 d​ 个潜在因子和 k​ 个生成因子，第 ij​ 项是仅使用第 i​ 个潜在因子 [\mu_{\phi}(x)]_i​ 预测的第 j​ 个因子的线性回归或者分类得分。对于回归，将其作为通过拟合一条最小化线性回归误差的直线(斜率和截距)得到的 R^2​ 分数 \left(\frac{\operatorname{Cov}\left(\left[\boldsymbol{\mu}_{\phi}(\mathbf{x})\right]_{i}, \mathbf{y}_{j}\right)}{\sigma_{\left.\mid \mu_{\phi}(\mathbf{x})\right]_{i}} \sigma_{\mathbf{y}_{j}}}\right)^{2}​ ，值域范围为[0,1]，得分为1，则表明第 i​ 个潜在因子的线性函数解释了第 j​ 个生成因子的所有变化；对于分类，对平衡分类误差最小的测试示例在第 i​ 个推断潜在因子上直接拟合一个或多个阈值(实数)，并取 S_{ij}​ 为第 j​ 个生成因子的平衡分类精度。对于某些维度有 \sigma[\mu_{\phi}(x)]_i=[Cov_{p(x)}[\mu_{\phi}(x)]_i]_i​ 接近0，则取 S_{ij}​ 为0。

对于对应一个生成因子的得分矩阵的一列，取前两项的差值(对应前两项最具有预测性的潜在因子的维度)的平均值作为最终的 SAP 分数，仅仅考虑每个生成因子的最高潜在因子是不够的，因为它不排除该生成因子被其它潜在因子捕获的可能性，高的 SAP 分数表明每个生成因子主要只被一个潜在因子捕获，但并不排除一个潜在因子捕获多个生成因子，并且多个潜在因子可能与同一个生成因子密切相关，对于这样的模型，使用单个潜在因子遍历生成示例不现实，而 SAP 得分可以根据相关性对潜在因子维度进行分组，由此得到分组级别的得分矩阵作为第二步的输入，并由此得到最终的 SAP 分数。

DCI(Disentanglement Completeness and Informativeness)

原文：A Framework for the Quantitative Evaluation of Disentangled Representations

方法

为了实现评测方法，文章使用了以下步骤：

  • 通过具有生成因子 z​ 的数据集训练模型 M​ ；
  • 为数据集的每个样本 x 检索 c ( c=M(x) )；
  • 训练一个回归模型 f ，对于给定的 c 去预测 z ( \hat z=f(c) )；
  • 量化 f 与理想映射的偏差和预测误差。

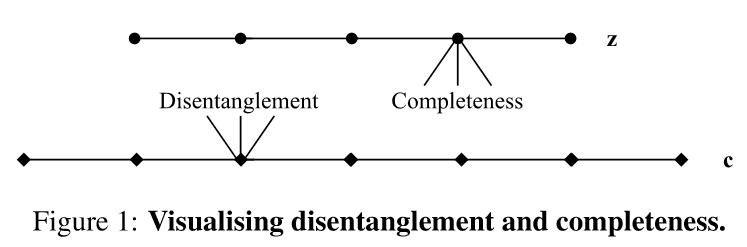
文章考虑了表征的三个属性，即解纠缠性、完整性和信息量。

解纠缠性：用来表示一个表征对变化因子的解纠缠程度，每个变量(或维度)最多捕获一个生成因子。

编码向量 c_i​ 的解纠缠分数定义为：

D_i=1-H_K(P_{i.})

其中 H_{K}\left(P_{i .}\right)=-\sum_{k=0}^{K-1} P_{i k} 表示熵， P_{i j}=R_{i j} / \sum_{k=0}^{K-1} R_{i k} 表示 c_i 预测为 z_j 的重要性概率，如果 c_i 对于预测一个单生成因子很重要，则分数为1，如果对所有生成因子一样重要，则分数为0。

为了计算 c​ 中dead或者无关的单元，使用相对编码向量重要性 \rho_{i}=\sum_{j} R_{i j} / \sum_{i j} R_{i j}​ 来构建一个表示总体解纠缠性的加权平均 \sum_{i} \rho_{i} D_{i}​ ，如果编码向量 c_i​ 跟预测的 z​ 无关，则 \rho_i​ 趋近于0。

完整性：用来表示单个编码变量捕获每个潜在因子的程度。

捕获生成因子 z_j 的完整性分数定义为：

C_{j}=\left(1-H_{D}\left(\tilde{P}_{. j}\right)\right)

其中 H_{D}\left(\tilde{P}_{. j}\right)=-\sum_{d=0}^{D-1} \tilde{P}_{d j} \log _{D} \tilde{P}_{i j} 表示分布 \tilde{P}_{i j} 的熵，如果一个单编码向量给预测 z_j 做贡献，则分数为1，如果所有的编码向量都对 z_j 的预测做贡献，则分数为0。

信息量：用来表示所捕获的变化因子的表征的信息量。

关于生成因子 z_j​ 的编码 c​ 的信息量定义为数据集的平均预测错误 E\left(z_{j}, \hat{z}_{j}\right)​ ，其中 E​ 是一个合适的误差函数，且 \hat{z}_{j}=f_j(c)​ ，信息量的度量依赖于 f​ 的能力，也依赖于将 c​ 表征为 z​ 的信息的模型的能力，因此信息量度量与解纠缠度量有一定重叠，重叠大小取决于 f​ 的能力。

Modularity

原文：Learning Deep Disentangled Embeddings with the F-Statistic Loss

对于Modularity，首先计算每个编码维度和每个因子之间的互信息，如果编码维度 i 理想的Modularity，则它与单个因子的互信息很高，与所有其它因子的互信息为0。于是使用与这种理想情况的偏差来计算Modularity的得分，给定单个编码维度 i 和因子 f ，用 m_{if} 表示编码和因子的互信息，其中 m_{if}\ge0 ，创建一个与 \mathbf{m}_i 具有相同大小的模板向量 \mathbf{t}_i ，它表示代码维度 i 在理想化情况下的最佳匹配情况：

t_{i f}=\left\{\begin{array}{ll} \theta_{i} & \text { if } f=\arg \max _{g}\left(m_{i g}\right) \\ 0 & \text { otherwise } \end{array}\right.

其中， \theta_i=\text{max}_g(m_{ig})​ ，所观察到的与模板的偏差为：

\delta_{i}=\frac{\sum_{f}\left(m_{i f}-t_{i f}\right)^{2}}{\theta_{i}^{2}(N-1)}

其中 N​ 是因子的个数，偏差0表示实现了完美的Modularity，1则表示该维度与各因子具有相等的互信息。由此使用 1-\delta_{i}​ 表示编码维度 i​ 的modularity score， 1-\delta_{i}​ 在 i​ 上的平均值作为所有编码的modularity score。这个值并没有告知每个因子在编码中是否都得到了很好的表示，为了确定编码的覆盖范围，需要explicitness度量。

假设因子为离散值，可为每个因子的每个取值计算一个explicitness score，在explicitness表示中，应该可以使用简单的分类器从编码中恢复因子的值。文章用一个one-versus-rest的logistic回归作为分类器，将整个编码作为输入，记录该分类器的AUC，使用 \text{AUC}_{jk} 在因子index j 和因子 j 的值的index k 上的平均值作为编码的explicitness score。

IRS(Interventional Robustness Score)

原文：Robustly Disentangled Causal Mechanisms: Validating Deep Representations for Interventional Robustness

Locatello论文的相关评测方法实验设置

原文：Challenging Common Assumptions in the Unsupervised Learning of Disentangled Representations

BetaVAE metric

Higgins et al.固定一个随机因子的变化，采样两个mini-batch的观测样本 \mathbf{x} ，最后测量线性分类器的准确率来衡量解纠缠性能，该线性分类器基于两个mini-batch的表征之间的绝对差的坐标和，预测固定的因子的index。实验时设置batchsize为 64 ，两个batch的一个随机因子固定在一个随机采样值，其它变化因子随机。计算这些样本点的平均表征并计算两个batch数据之间的绝对差值，再将这 64 个值平均，形成一个训练(或测试)点的特征，默认使用 10000 个样本训练logistic regression， 5000 个样本测试。

FactorVAE metric

Kim & Mnih改用多数投票分类器，该分类器基于具有最小方差的表征的index来预测固定的真值因子的index。实验时首先采样 10000 个随机样本估计每个潜在维度的方差，并排除方差小于 0.05 的崩塌维度；其次设置batchsize为 64 ，每个batch的一个随机因子被固定为相同的随机值，来生成多数投票分类器的选票；最后计算其潜在表征的每个维度的方差，并除以在无干预情况下计算的数据的方差。多数投票分类器的训练点由归一化方差最小的维度的index组成，训练时采用 10000 个样本，测试时采用 5000 。

Mutual Information Gap

Chen et al.表明BetaVAE metric和FactorVAE metric依赖于一些超参数，不通用且不是无偏的。通过计算每个真实因子和每个计算表征 r(\mathbf{x}) 的维度之间的互信息，对于每个真实因子 \mathbf{z}_k ，考虑 r(\mathbf{x}) 中与 \mathbf{z}_k 具有最高和次高的互信息的两个维度。MIG定义为各因子(数量为表征的维数)的最高和次高互信息的平均归一化差值。原始的方法使用采样表征，本文为了跟其它方法保持一致，则使用平均表征。实验将得到的 10000 个样本的表征离散化到 20 个bins，由此计算离散的互信息，该指标分数计算如下：

\frac{1}{K} \sum_{k=1}^{K} \frac{1}{H_{z_{k}}}\left(I\left(\mathbf{v}_{j_{k}}, \mathbf{z}_{k}\right)-\max _{j \neq j_{k}} I\left(\mathbf{v}_{j}, \mathbf{z}_{k}\right)\right)

其中， \mathbf{z}_k 是一个变化因子， \mathbf{v}_j 是潜在表征的一个维度， j_k=\text{arg max}_j I(\mathbf{v}_j,\mathbf{z}_k) 。

Modularity

Ridgeway & Mozer表明应该考虑两个不同的属性：Modularity和Explicitness。对于Modularity， r(\mathbf{x}) 的每个维度最多只取决于一个变化因子；对于Explicitness，变化因子的值应该很容易从 r(\mathbf{x}) 中预测出来。原文提出用变化因子和 r(\mathbf{x}) 的维度的最高互信息和次高互信息的平均归一化平方差来衡量Modularity，使用一个one-versus-rest的logistic回归分类器的ROC-AUC来测量Explicitness。对于modularity score，实验采样 10000 个数据点，从中获得潜在表征，再将这些点离散到20个bin中，并计算表征和变化因子值之间的互信息，得到 \mathbf{m} 。对于每个表征的维度 i ，计算得到向量 \mathbf{t}_i ：

t_{i f}=\left\{\begin{array}{ll} \theta_{i} & \text { if } f=\arg \max _{g}\left(m_{i g}\right) \\ 0 & \text { otherwise } \end{array}\right.

其中， \theta_i=\text{max}_g(m_{ig}) ，modularity score为 1−\delta_i 在表征维度上的平均值：

\delta_{i}=\frac{\sum_{f}\left(m_{i f}-t_{i f}\right)^{2}}{\theta_{i}^{2}(N-1)}

其中 N 是因子的个数。

DCI Disentanglement

Eastwood & Williams考虑表征的三种属性，即Disentanglement,Completeness和Informativeness。首先计算了学到的表征的每个维度对预测变化因子的重要性， r(\mathbf{x}) 每维的重要性可以用Lasso或者Random Forest分类器计算。Disentanglement是学习表征的一个维度对于预测一个因子有用的概率的熵的平均值，该因子的值是每个维度的相对重要性；Completeness是一个变化因子被一个维度的学习表征捕获的概率的熵的差值的平均值；Informativeness则是预测变化因子的预测误差。实验分别采样 10000 个训练样本和 5000 个测试样本，对于每个因子，使用gradient boosted trees的Scikit-learn的默认设置。从该模型中提取特征维度的重要性权值，取绝对值构成重要性矩阵 R ，其行对应于因子，列对应于表征。为了计算disentanglement score，首先从这个矩阵的每一列的熵中减去 1 (将列归一化作为一个分布对待)，由此得到一个长度等于潜在空间维数的向量，然后再计算每个维度的相对重要性： \rho_{i}=\sum_{j} R_{i j} / \sum_{i j} R_{i j} ，最后disentanglement score为 \sum_{i} \rho_{i} (1-H(R_{i})) 。

SAP score

Kumar et al.提出计算线性回归的 R^2 分数，该线性回归从学习的表征的每个维度预测因子值。对于离散因子，则训练一个分类器。Separated Attribute Predictability score是各因子预测误差最大的两个潜在维度的平均差值。实验采样 10000 个数据点训练，使用 5000 个样本测试，然后计算一个包含测试加预测误差的分数矩阵，该分数矩阵用于 C=0.01 的Linear SVM，其从单个潜在维度去预测因子的值。SAP score则计算最具预测性的两个潜在维度之间的差值的平均值。

相关文章