动机
- 表示学习使机器学习模型能够解读数据中潜在的语义,并对隐含的变化因子进行解纠缠,使得对于不同的任务进行知识迁移变得可能,但是是什么让一种表征比另一种更好呢?
- 在数据密集型领域中,表示学习的通用先验之一就是聚类,虽然聚类主要的重点是将原始数据分到类中,但如果在降维的过程中获得真实数据的低维数据流形更好;
- 生成模型的许多应用是基于隐空间的,对于GAN隐空间的解纠缠使得GAN与缺乏可解释性的传统降维技术区分开来,即希望隐空间既要有聚类性,也要有良好的可解释性和插值能力。
贡献
- 证明了虽然GAN的隐变量保留了观测数据的信息,但隐空间中的点是基于平滑分散的潜在分布,导致没有可观测的簇,即GAN的隐空间中并没有保留聚类的结构;
- 提出了一种新的GAN的聚类框架ClusterGAN,通过从离散编码向量和连续编码向量的混合变量中采样隐变量,提出了一种新的处理离散-连续混合问题的反向传播算法,再结合特定聚类损失的逆网络,实现隐空间聚类;
- 实验结果表明,GAN能够保留跨类别的隐空间插值,即使判别器并没有接触到这些向量,同时对于聚类任务有很好的结果。
离散-连续先验
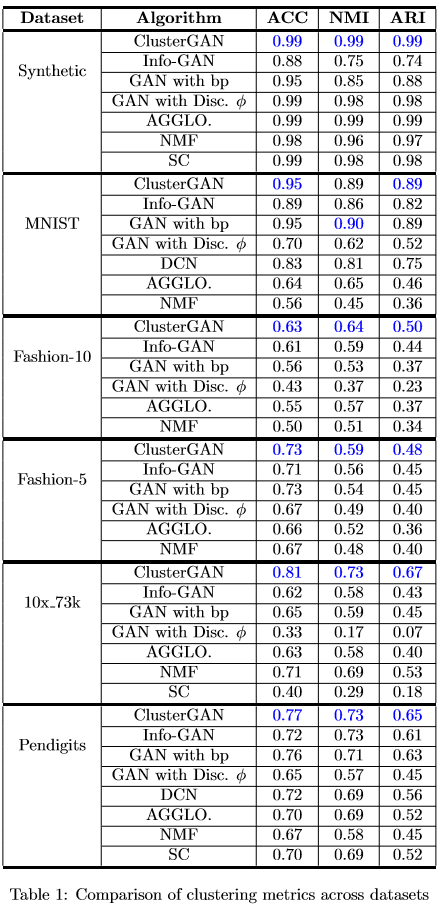
标准GAN在隐空间不能很好的聚类
使用GAN进行聚类的一种可能方法是将数据反向传播到隐空间并在隐空间中进行聚类,然而现有方法结果非常差,关键的原因在于如果反向传播成功了,则反向投影的数据分布应该跟隐空间的分布相似,但隐空间通常选择高斯分布或均匀分布,不能期望在该空间中进行聚类(由下图可以看出)。
利用分类变量提升空间可以有效地解决这一问题,但是隐空间的连续性传统上被认为是实现良好插值目标的先决条件,即插值似乎跟聚类存在一定的矛盾,而本文的方法证明了ClusterGAN能同时获得良好的插值和聚类效果。
从离散-连续混合变量中采样
在ClusterGAN中,从一个级联的正态随机变量和一个one-hot编码向量的先验中采样,即,其中,,是中的第个基本向量,且是数据中的簇数,本文对于所有实验,设置,使得正态隐变量,任意有一个高概率,而为了保证空间的分离,选择了小的方差。
基于译码的修改的反向传播

线性生成器能完美聚类
引理:仅用聚类无法在线性生成空间中恢复高斯混合数据,进一步,存在一个线性生成器映射从离散-连续混合到高斯混合。
这个引理表明,在离散-连续混合的情况下,只需要线性生成就可以在生成空间中生成混合高斯函数。
本文的方法
网络由生成器,判别器,编码器组成,编码器用于精确恢复潜在向量。训练过程中首先从离散连续分布中采样,通过生成器G生成fake-image,将fake-image分别输入到判别器D和编码器E中,在D中判别,在E中将fake-image反向解码为和。
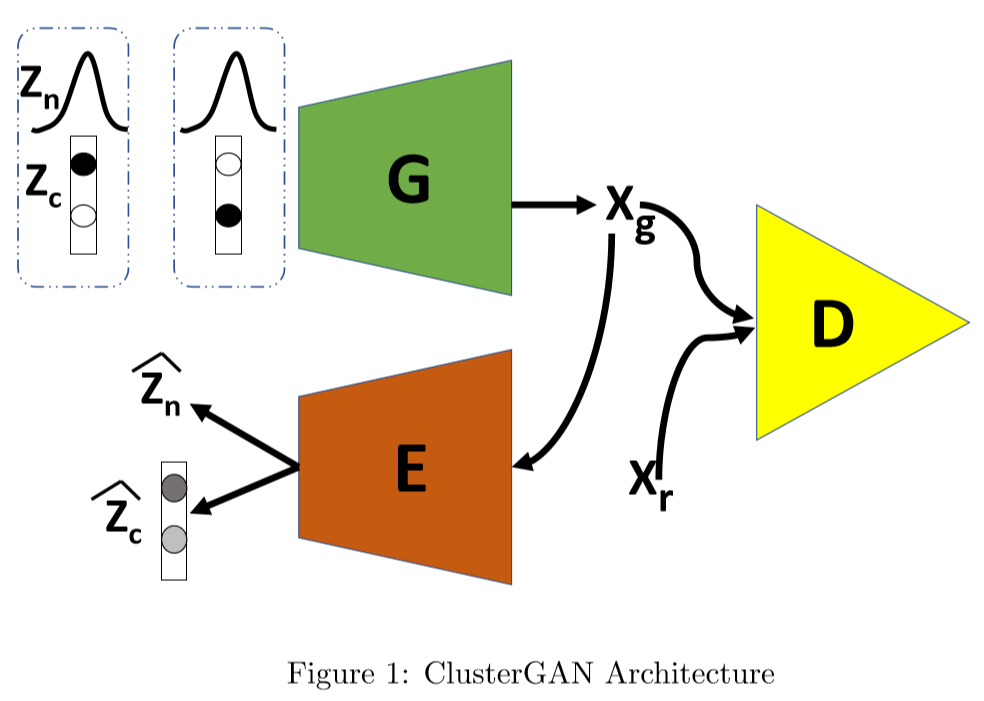
尽管上述方法使GAN能够在隐空间中进行聚类,但如果在极大极小目标函数中有一个聚类特定损失项,它可能会表现得更好。确保在复杂的数据集的聚类,强制精确地恢复隐向量,因此引入一个编码器E,GAN的损失函数为:
其中是交叉熵损失,正则化系数和的相对大小能灵活地选择改变保留隐编码的离散和连续部分的重要性。其它正则化的变体诸如将映射到各自的聚类中心附近,例如,类似于K-Means。在本文中,使得接近且接近,GAN训练如下图同时更新和。

部分实验结果

上图表示本文方法可以将数据中不同类的不同模式解纠缠。

上图表示本文方法具有良好的插值能力。