
动机
- 流行的无监督学习框架-表示学习的目的是使用无标签的数据学习一个表示,以揭露重要的语义特征作为容易解码的因子,使得对下游任务有用;
- 为了发挥作用,一个无监督的学习算法必须在不直接接触下游任务的情况下正确地猜测可能地任务集,出于对创建的观测数据需要的某种形式的理解,常希望生成模型自动学习解纠缠的表示;
- GAN使用一个连续的输入噪声,同时对生成器可能使用这种噪声的方式没有限制。因此,生成器可能会以一种高度纠缠的方式使用噪声,导致的单个维度与数据的语义特征不一致。
贡献
- 提出了一种无监督的GAN框架InfoGAN,通过最大化隐变量的一个子集与观测之间的互信息,推导出了可有效优化的互信息目标函数下界;
- 实验表明InfoGAN学习的可解释性表示与现有的监督方法学习的表示具有竞争性。
诱导隐编码的互信息
GAN使用一个连续的输入噪声,同时对生成器可能使用这种噪声的方式没有限制。因此,生成器可能会以一种高度纠缠的方式使用噪声,导致的单个维度与数据的语义特征不一致。
但是许多域会自然地分解为一系列语义相关的变化因子,比如MNIST数据集,理想情况下希望模型能够自动选择出对应数字类别(0-9)的离散变量,并选择两个额外的连续变量表示数字的角度和粗细。
所以本文将输入的噪声向量分解为两部分:不可压缩噪声和学习数据分布的结构化语义特征的隐编码,即生成器的分布变成了,而标准GAN忽略了隐编码,所以需要找到一种解决方法满足,本文提出了一种信息论正则化方法:即隐编码和生成器分布之间应该有较高的互信息量。
对于互信息的定义,其中表明观测到随机变量时,的不确定性减少的程度,即如果和由一个很强的可逆的函数关联,则会有很大的互信息量,所以不希望隐编码中的信息在生成过程中丢失,所以损失函数为:
变分互信息的最大化
很难直接通过先验去求解,所以采用定义一个辅助分布去近似:
本文直接将隐编码固定,故直接作为一个常数。同时由引理,对于随机变量,和函数,,得到互信息的变分下界:
其中比较容易使用蒙特卡洛模拟来近似,并且可以用重参数化技巧来直接最大化和,所以最后InfoGAN的损失函数为:
实现
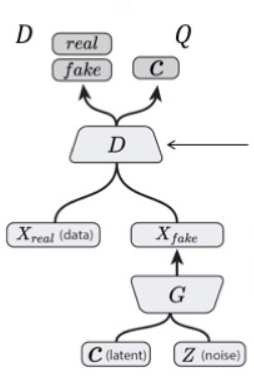
将辅助分布作为一个神经网络,其中和共享所有卷积层,并通过一个全连接层输出参数的条件分布,对于类别隐编码,使用softmax来选择,对于连续隐编码,本文使用一个高斯函数来表示,本文是基于DCGAN来做的实验。
部分实验结果
互信息最大化
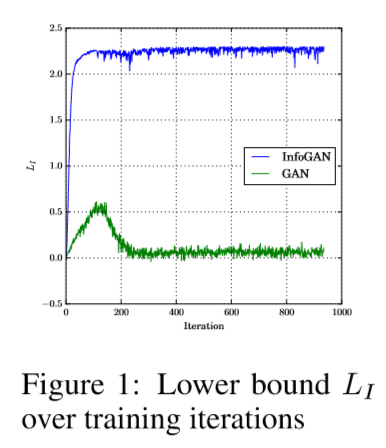
通过上图发现,对于标准GAN而言,隐编码跟生成的图像之间几乎没有互信息,说明标准GAN不能保证生成器在利用隐编码。
解纠缠表征

实验设置:包含离散的类别编码,连续编码分别代表角度和字体粗细。由上图可以看出,其解纠缠的能力很出色。



