动机
- 学习与变化的潜在因素相一致的表征对于可解释的和人工干预的机器学习至关重要,且现在的方法从无监督的方法向弱监督方法转变,但目前还没有相关论文去确定弱监督在何时以及如何保证解纠缠,即对于不同形式的弱监督所提供的理论保证,并没有形式上的描述。
贡献
- 提供了一种理论框架帮助分析弱监督学习方法所带来的解纠缠能力,即将弱监督学习形式化为扩展空间中的分布匹配;
- 受到先前工作的启发,提出了一组可以处理相关因子的解纠缠定义,并由此提出了一种解纠缠的理论推导;
- 利用提出的理论框架,通过实验分析了几种弱监督方法(restricted labeling,match-pairing,rank-pairing)的保证和局限性,表明虽然某些弱监督方法(如在风格内容解纠缠中的风格标签)不能保证分离,但通过多个弱监督源结合时,本文的推断是可以保证解纠缠的。
从无监督到弱监督分布匹配
解纠缠学习的目标是得到一个隐变量生成模型,生成对应于数据中真实变化因子的隐变量。为了验证无监督方法在解纠缠上的保证,首先形式化考虑的模型族,弱监督的形式,最后使用评估方法验证和证明解纠缠的成分。
对于数据生成的过程,可以认为变化因子为其分布为,而是观测到的数据点,并且有,现存的无监督方法是希望去学到一个带先验的隐变量模型和一个生成器,使得,但是,仅仅匹配数据的边缘分布是不够的。
所以目前的方法转变为弱监督,其中数据生成过程的信息是通过额外的观测来传递的,通过在增广空间上(而不是观测X)上执行分布匹配来保证表征学习的监督。
现有的弱监督方法的形式

所有这些监督形式可以被认为是原始联合分布的增广形式,将隐变量划分为,要么观察隐变量的一个子集,要么在多个样本中共享隐变量。
restricted labeling
通过观测真实因子的一个子集,即,这允许在上执行分布匹配,即是数据和可观测的因子的联合分布,而不只是数据,这种形式的监督经常在风格-内容分离中使用,其中标签可用于内容,但不能用于样式。
match pairing
使用成对的数据共享一个已知因子的子集,对于许多数据模式,变化的因子很难被标记,但收集具有相同潜在因子的成对样本可能更容易(例如收集不同人戴同一副眼镜比为眼镜风格定义标签更容易)。匹配配对是一种较弱的监督形式,因为学习算法不再依赖于潜在的值,而仅依赖于共享因子的标记。
rank pairing
一个额外的标记变量被观测决定是否对应的隐变量比好:,适用于比较两个样本的潜在因子比直接收集标签更容易时(例如比较两个物体的大小和提供一个标尺测量一个物体),本文重点关注在解纠缠保证上下文的排名配对。
所以可以使用采样自ground truth模型的数据和分布匹配目标来训练生成模型,比如:对于match pairing,训练一个生成模型,这样来自生成器的成对随机变量,匹配来自增广数据分布对于的成对随机变量
定义解纠缠
本文将解纠缠分解为两个不同的概念:一致性和限制性,不同形式的弱监督可以使因子子集具有这两种性质。
将解纠缠分解为一致性和限制性
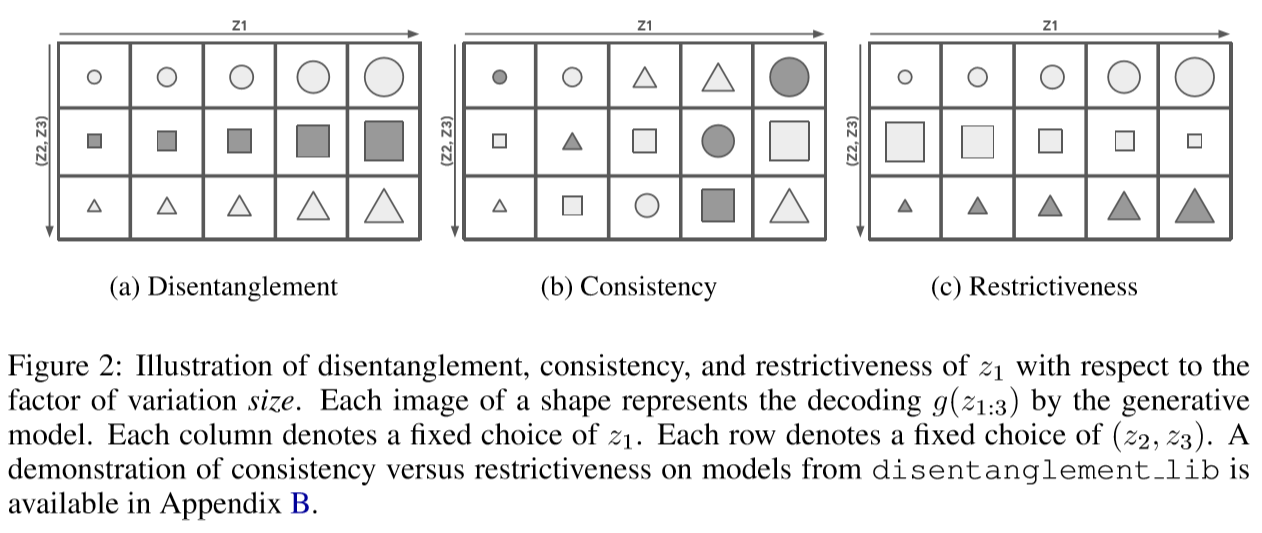
考虑一个真实模型,它由变化因子(size , shape , color )生成形状,对于如何确定生成模型将表示size的解纠缠了?直观上是检查当改变时是否发生上图(a)的变化,即:当固定时,生成目标的不会改变;当只有改变时,即只有改变,其它的不变。
假设数据生成函数已经得到,设是生成模型的假设类,是一个元组,其中描述了变化因子的分布,生成器是一个表示因子空间到观测空间的映射函数,编码器是一个表示的映射函数,对做了一个温和的假设,假定每一个变化因子都能从观测恢复回来,即。
给定一个oracle模型,希望去学习一个模型的隐变量能够解纠缠的隐变量,如果进一步限制,即
生成器一致性
表示示例的集合,而表示生成的过程:
即生成过程从采样一次,条件采样两次,则希望和具有一致性:
其中是受限于的oracle编码器,上式表明,对于任意选择的,重采样不会影响oracle对因子的测量,即不随着的改变而改变,即上图(b)每一列,大小不变。
生成器限制性
表示生成过程,则:
如果被限制为,即:
上式表明对于任意选择的,对的重采样不会影响对oracle因子的测量。即对于的变化是不变的,如上图(c)的每一行,图像样式和颜色没有改变。
生成器解纠缠
如果与一致且受限于,则说明解纠缠,即:
用于解纠缠的基于编码器的定义
编码器一致性
表示生成的过程:
即生成过程从采样一次,条件采样两次,则希望和具有一致性:
作者由此得到两个结论:
- 只要能够访问来自oracle生成器的配对数据,就可以检查编码器的一致性/限制性/解纠缠性,这与现有的解纠缠定义和度量形成了对比,现有方法需要访问真实的因子(个人猜测是指本文方法不需要相互独立);
- 在对生成数据进行测试时,基于编码器的定义是可以测量的,因为生成数据直接服务于oracle生成器,后续发展理论以保证基于生成器和基于编码器的解纠缠时,实验均是针对一个训练的编码器进行的。
本文定义了三个概念:;表示为true;隐含的依赖于(基于生成器)或(基于编码器)
解纠缠的推断
首先由定义等价于,其次由前面的图可以看出和不互相隐含,于是乎探讨对某些变量集的一致性或限制性是否意味着是其他变量集合的附加属性。

不再需要去证明有监督的方法是否对每个因子都满足一致性和限制性,只需说明一种监督方法保证了一个因子子集的一致性和限制性,再通过完全解纠缠的推断来组合多个监督方法,本文证明了当弱监督只对一部分变量子集适用时,能发现独立因子的一致性或限制性,比如和的一致性可以推断出的一致性。
将带担保的弱监督形式化
本节讨论解纠缠是由有监督方法或者是模型归纳偏置引起的,由Locatello等人证明无监督方法验证依赖模型归纳偏置,所以重点探讨弱监督方法带来的解纠缠意味着什么。
定义的关键是促使策略和学习算法对处理所有由假设类引出的oracle,由此避免模型的归纳偏置,因为的任何偏置会减少假设类导致无法在互补假设类处理oracle。
弱监督方法的分析
将本文的理论框架应用于上文提到过的三种弱监督方法,发现:这些方法可以提供单因子的一致性或限制性保证;同时通过对所有因子施加一致性或限制性,可以学习具有较强解纠缠能力的模型。
弱监督方法的理论保证
如果一个训练算法成功地将生成的分布与通过因子生成的数据分布进行匹配,则就能保证与的一致性:

定理1指出对于基于几种弱监督方法的的分布匹配保证了生成器和编码器的一致性,并且可以由来保证受限于,但相同的监督不能保证受限于(定理2)。然而如果额外使用restricted labeling或者match pairing的,能够推断出,由此对因子解纠缠。
实验
单因子实验
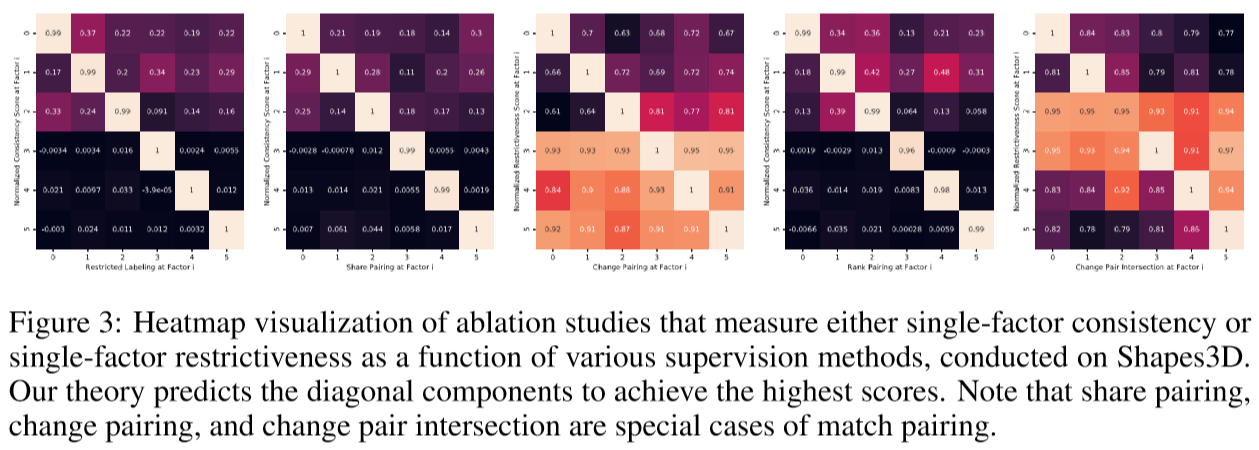
表明本文的理论可以有针对性地保证单因子的一致性或限制性。
一致性与限制性实验
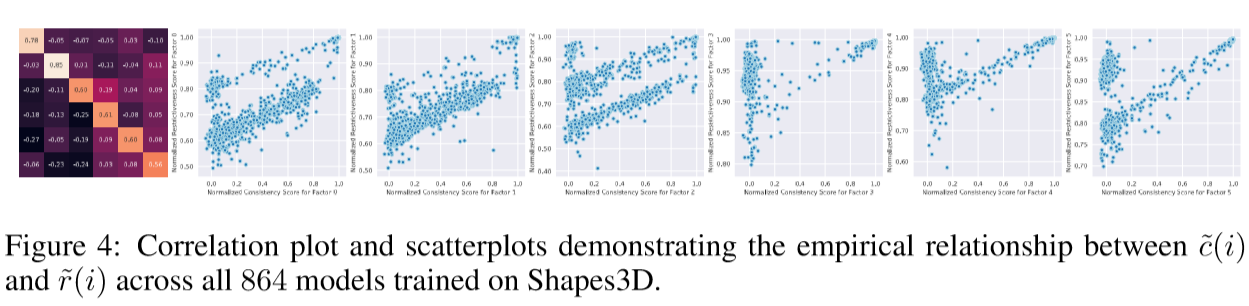
展示了单因子一致性与限制性之间的关联程度,即使模型只被训练为最大化其中一个。
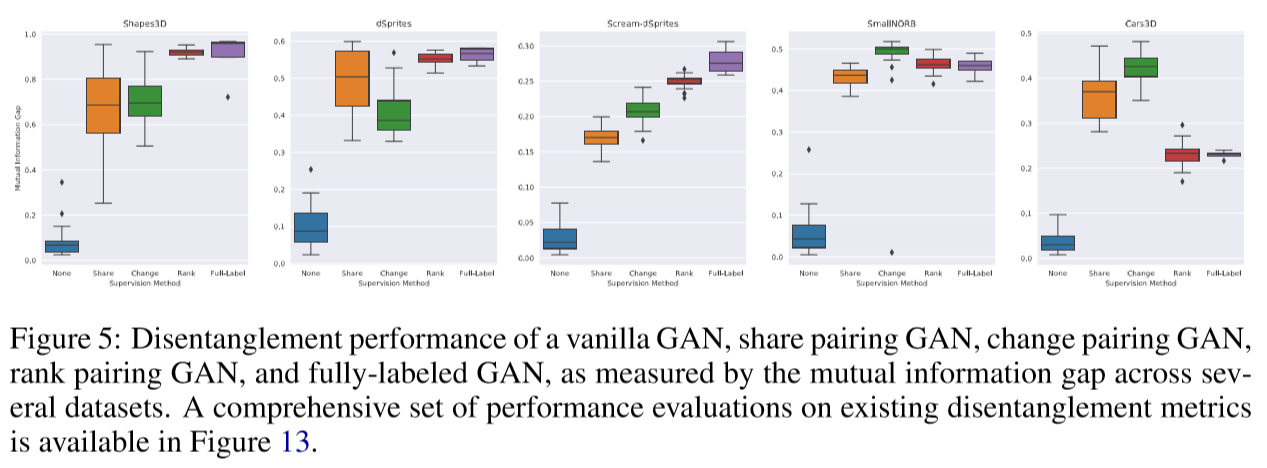
完全解纠缠实验