You got a dream, you gotta protect it.

0%

论文阅读-disentanglement-Disentangling factors of variation using few labels

发表于 分类于 Valine： 本文字数： 4.2k 阅读时长 ≈ 4 分钟
用少量标签解开变化因子

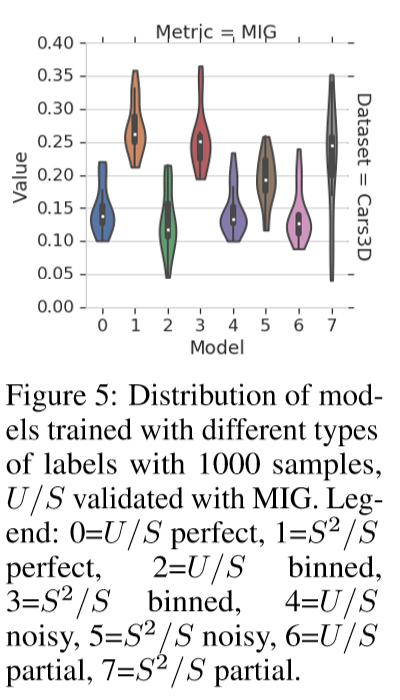
动机

  • Locatello等人证明无归纳偏置的无监督解纠缠学习在理论上是不可能的，现有的归纳偏置和无监督方法不足以持续学习解纠缠表征；
  • 但是实际环境中，往往只能得到有限的监督，如通过对少量训练实例中的(部分)变化因素进行人工标注。

贡献

  • 观测到一些现有的解纠缠策略(需要 z 的观测)能够在极少量标签的情况下，调整无监督方法的超参数，而具有较好的效果，因此训练各种模型并引入监督去进行模型选择是一个可行的解决方法；
  • 发现添加一个简单的监督损失(即使只使用100个有标签样本)将标签信息加入到训练中去，在解纠缠的分数和下游任务上都比带有监督验证的无监督训练方法更好；
  • 发现带有监督验证的非监督训练方法和半监督训练方法对噪声标签有较好的鲁棒性，并且可以容忍粗糙和局部的注释。

本文介绍

目前最好的无监督解纠缠方法使用不同的无监督正则化去丰富VAE的目标，旨在鼓励解纠缠表征。这些方法表现形式上有很大的差异，能够较好的解纠缠但很难在无监督的情况下一致，这与Locatello等人的理论结果一致，即无归纳偏置的无监督解纠缠学习在理论上是不可能的。

其它方式的归纳偏置如依赖时间信息(视频数据)，允许与环境进行交互，或合并分组信息等，会具有更高的时间消耗与计算成本，相比之下，收集少量标签显式地将先验知识和偏置编码到学习的表征中更好。

首先，本文分析了解纠缠的分数对于不精确的标签是否对样本有效和具有鲁棒性；其次探讨是否将有限数量的标签纳入到训练中更有利，并平衡这种方法和有监督验证，发现带有监督验证的无监督训练能够使得解纠缠表征的可靠学习成为可能，同时对下游任务也更有益。

问题定义

机器学习通常假设高维观测 x (如图像)是一个低维隐变量 z 变换的表现，即通常假设这些隐变量存在一个分布 p(z) ，真实的观测 x 是通过从 p(z) 中采样得到 z ，再由条件分布 p(x|z) 生成的，解纠缠的目标则是找到一个能够独立捕获 z 中所有真实的变化因素的一个数据表征 r(x) ，即希望 z 的变化对应着 r(x) 的变化，然后希望这样的表征是可解释的，最大限度简洁的且对下游任务有用的。

评估解纠缠表征

BetaVAE和FactorVAE通过对变化因子进行干预并预测哪些因素被干预来测量解纠缠；Mutual Information Gap(MIG)、Modularity、DCI Disentanglement和SAPscore首先计算一个与变化因子和编码相关的矩阵(例如通过两两互信息、特征重要性和可预测性)，然后，求矩阵的前两个元素行或列的标准化差的平均值(具体说明见文章附录)。

学习解纠缠表征

因为所有的度量都需要标签 z ，所以它们不能用于无监督的训练。因此，许多无监督解纠缠方法使用正则化器 R_u(q_{\phi}(z|x)) 去扩展VAE，在VAE的隐空间强化结构以期望获得解纠缠表征的编码分布 q_{\phi}(z|x) ，常通过以下优化模板进行转换(具体说明见文章附录)：

\underset{\phi, \theta}{\max } \underbrace{\mathbb{E}_{\mathbf{x}}\left[\mathbb{E}_{q_{\phi}(\mathbf{z} \mid \mathbf{x})}\left[\log p_{\theta}(\mathbf{x} \mid \mathbf{z})\right]-D_{\mathbf{K L}}\left(q_{\phi}(\mathbf{z} \mid \mathbf{x}) \| p(\mathbf{z})\right)\right]}_{=: \operatorname{ELBO}(\phi, \theta)}+\beta \mathbb{E}_{\mathbf{x}}\left[R_{u}\left(q_{\phi}(\mathbf{z} \mid \mathbf{x})\right)\right]

带有监督模型选择的无监督训练

本节将研究如果有少量标记的观察数据可用，是否可以使用常用的解纠缠度量来识别好的模型。

实验表明注释100-1000个数据点并使用它们来获得一个解纠缠的表示是可行的，但与此同时不清楚这种度量方法是否有效，因为现有的度量方法已被发现是有噪声的，最后观测到来自 z 的样本表示Locatello的不可能结果并不适用于此设置。

实验设置和方法

数据集

dSprites，Cars3D，SmallNORB，Shapes3D，对于每个数据集，假设有100或1000个可用的标记示例和大量未标记的观测值。

完美vs不精确的标签

除了使用真实标签，本文还考虑了标签不精确的情况，即标签被丢弃，最多取5个不同的值，是有噪声的(每一个变化因子的观测值有10%的概率是随机的)或部分的(只有两个随机的变化因子被标记)。

模型选择的策略

本文使用MIG、DCI Disentanglement和SAPscore作为评估标准。

实验设定

本文考虑了32种不同的实验设置，其中一个实验设置对应于一个数据集(4种)，一个是标记示例的数量(2种)，以及一个标记设置(4种，perfect/binned/noisy/partial)。

实验发现

观测发现：使用MIG和DCI的100个标记示例的DCI解纠缠方法，可以在这些数据集上良好运行，而且即使没有准确的标签，指标也是可靠的。所以在实践中，标记少量的示例，以监督验证是一个合理的学习解纠缠的方法，同时发现用更粗糙的方式标记更多的变化因子比更准确地标记更少地变化因子更好。

在训练期间加入标签信息

本节将比较将少量的标签信息加入到现有的无监督解纠缠方法训练中和使用无监督训练有监督模型选择的方法。

关键想法是利用有限的标签信息去确保VAE的隐空间具有理想的结构，即在上文的无监督优化模板的基础上增加了一个约束 R_{s}\left(q_{\phi}(\mathbf{z} \mid \mathbf{x}), \mathbf{z}\right)\le k ，其中 R_{s}\left(q_{\phi}(\mathbf{z} \mid \mathbf{x}), \mathbf{z}\right) 是用来计算少量有标签观测的函数，通过KKT条件得到：

\max _{\phi, \theta} \quad \operatorname{ELBO}(\phi, \theta)+\beta \mathbb{E}_{\mathbf{x}} R_{u}\left(q_{\phi}(\mathbf{z} \mid \mathbf{x})\right)+\gamma_{\text {sup }} \mathbb{E}_{\mathbf{x}, \mathbf{z}} R_{s}\left(q_{\phi}(\mathbf{z} \mid \mathbf{x}), \mathbf{z}\right)

其中， R_{s}\left(q_{\phi}(\mathbf{z} \mid \mathbf{x}), \mathbf{z}\right)=-\sum_{i=1}^{d} z_{i} \log \left(\sigma\left(r(\mathbf{x})_{i}\right)\right)+\left(1-z_{i}\right) \log \left(1-\sigma\left(r(\mathbf{x})_{i}\right)\right) ，如果维度高于 d ，也只取前 d 维做正则化( d 是变化因子的个数)，用 L_2 损失的效果比交叉熵差。

后续作者通过实验去验证了一些想法，具体见论文第四节

是否应该将标签用于训练？

作者发现构建的半监督训练并没有直接提升解纠缠的分数，但相比带有监督选择的非监督训练会更好。同时标签越多，好处越大，找到非常有效的样本解纠缠度量是解纠缠实际应用的一个重要研究方向。

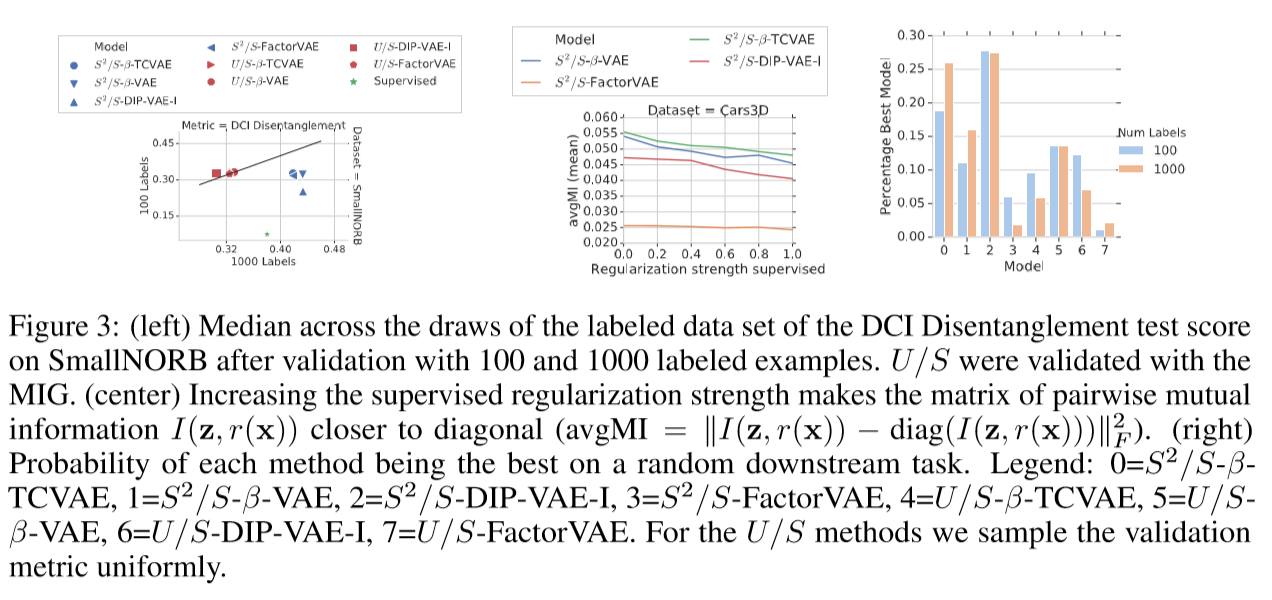
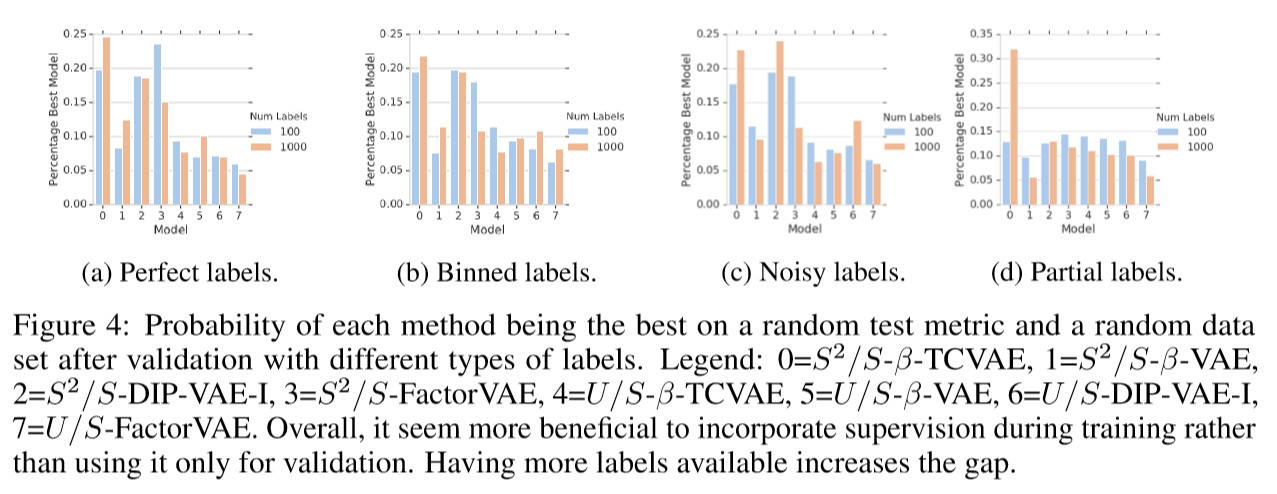
对于不精确的标签，半监督训练的鲁棒性有多好？

实验结果表明， S^2/S 方法对不精确的标签也有较强的鲁棒性，虽然 U/S 方法似乎更健壮，但 S^2/S 方法仍优于它们。

相关文章