动机
- 交叉熵损失是有监督分类模型中应用最广泛的损失函数,但交叉熵损失对噪声标签不鲁棒,且存在poor margins的可能性,而导致泛化性不好,而现有的改进方法不能很好的用于imagenet等数据集。
贡献
- 提出了一种新的对比损失函数,它允许对于每个anchor有更多的正样本,因此将对比学习应用在了有监督的学习;
- 同时实验证明,与交叉熵相比,这种新的损失提供了更好的准确性和鲁棒性;本文新的损失对超参数的敏感性不如交叉熵,是因为在嵌入空间,将同一类的点聚类在一起,对于不同类别的样本则分开,更有效地利用了标签地信息;
- 通过分析可以发现,本文的损失函数鼓励去学习hard positives and negatives,同时证明triplet损失是本文损失的一种特殊情况(当只有单个正负样本时)。
本文的方法
表征学习框架
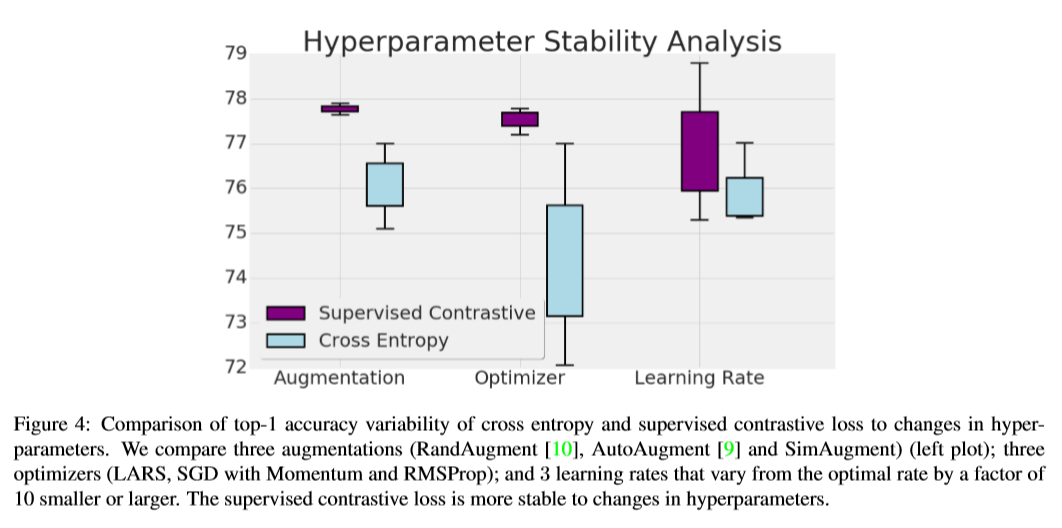
本文的表征学习框架在结构上类似于自监督对比学习的框架,由以下组成部分组成:
数据增强模块
将输入图像
x转换为随机增强的图像,对于每个输入图像,将生成两个随机增强的图像,每个图像代表数据的不同视图,因此包含原始输入图像中的一些信息子集。增强的第一阶段是对图像应用随机剪裁,再将其调整回图像的原始分辨率,第二阶段使用的数据增强方法有:AutoAugment,RandAugment,SimAugment编码器网络
将增广图像映射为一个表征向量,,本文将每个输入图像的两个增强图像分别输入到同一个编码器,从而产生一对表征向量,同时这个表征层通常被归一化为单位超球面,这与其他使用度量损失的方法一致,同时发现监督对比损失对于超参数的选择没那么敏感。
投影网络
将归一化表示向量映射成一个向量,最后再进行归一化,使用内积来计算投影空间中的距离,这个网络仅用来训练有监督的对比损失,训练完成后会被一个线性层取代。
对比损失
作者试图开发一种对比损失函数,该函数既允许有效地合并有标签的数据,同时也能保留对比损失的有益特性,通过随机采样数据的方式生成minibatches,从数据中随机采样个样本对,记为,是的标签,之后进行数据增强获得个数据样本,其中,和是分别用两种随机增强方法得到的数据对,而。
自监督对比损失
其中和表示同源的两种增强图像的索引,,P和E分别代表投影网络和编码器网络,通过点积计算相似度,意义在于拉近于其正对的距离而拉远与其他负对的距离。
监督对比损失
对于有监督的任务,自监督对比损失不能处理多个样本属于同一类的情况,所以本文扩展该损失函数,使得同一类的样本均为正样本:
其中是minibatch中相同标签的样本数,对比损失的核心是有足够多的负对,以便与正对形成鲜明的对比,同时增加了正对的数量,使得能够更好的刻画类内样本的相似性。
如上图,本文提出的监督对比损失分为两个阶段:在第一阶段,使用标签来选择图像的对比损失;在第二阶段,冻结已学习的表示,然后使用softmax损失在线性层上学习分类器。通过这两阶段从而结合使用标签和对比损失的好处。
监督对比损失的梯度传播
本文通过分析证明了监督对比损失其梯度,能促使网络更多的关注hard positives and negatives(即持续对比那些对编码器有较大好处的anchor),证明此处略。
与Triplet损失的联系
本文证明triplet损失是本文损失的一种特殊情况(当只有单个正负样本时)。
部分实验结果
通过比较监督对比损失和交叉熵损失情况下imagenet的分类准确率
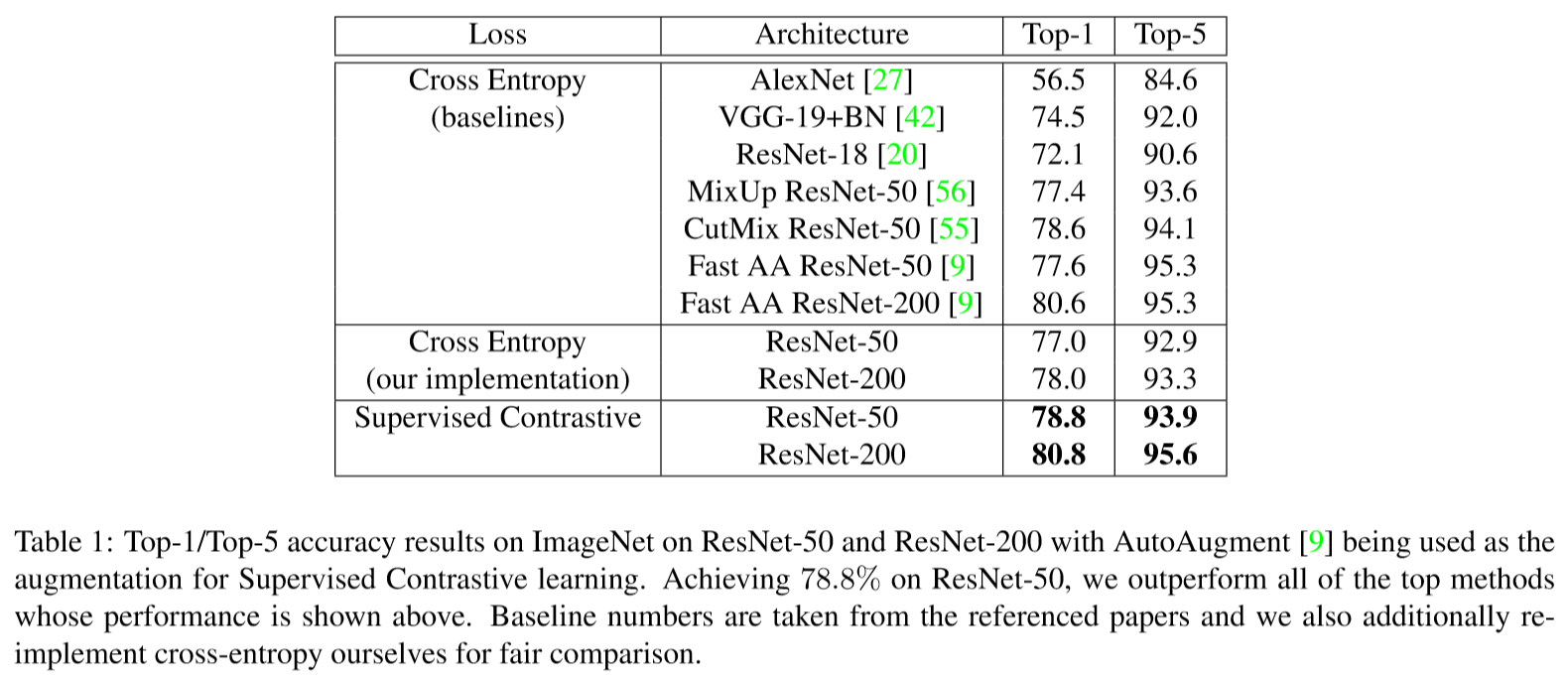
通过比较监督对比损失和交叉熵损失情况下对于有噪声扰动的imagenet的相对破坏误差和平均破坏误差(越小越好)
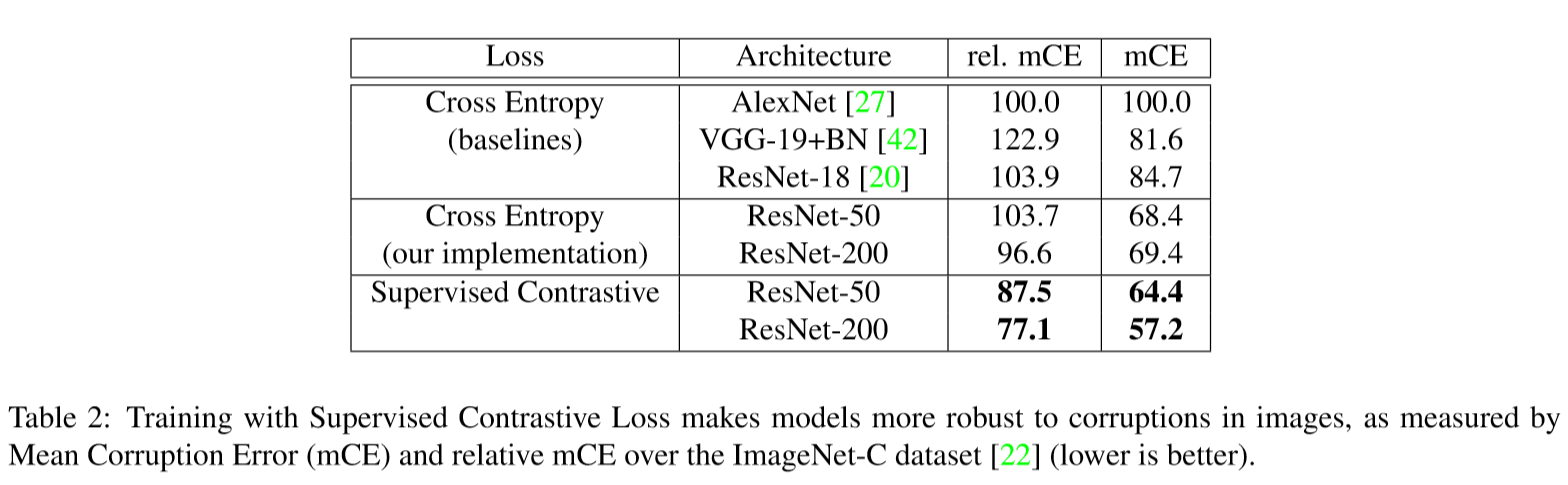
比较超参数设置对网络的影响