You got a dream, you gotta protect it.

0%

论文阅读-scene graph-Bridging Knowledge Graphs to Generate Scene Graphs

发表于 更新于 分类于 Valine： 本文字数： 9.4k 阅读时长 ≈ 9 分钟
连接知识图生成场景图

动机

  • 场景图将图像解析为语义元素，例如对象及它们之间的相互关系等，有助于视觉理解和可解释推理；常识图则编码世界是如何构造的以及一般概念是如何交互的；
  • 本文希望能在这两种构造之间搭建一个桥梁，将场景图看作是一个常识性知识图在图像条件下的实例，将场景图的生成重新表述为场景图和常识图之间的桥梁推理，其中场景图中的每个实体或谓词实例都必须链接到常识图中对应的实体或谓词类。

贡献

  • 提出了一种新的基于图的神经网络，它在两个图之间以及每个图之间迭代地传播信息，同时在每次迭代中逐步完善它们之间的桥梁。
  • 提出的图桥接网络GB-Net，通过连续推断边和节点，允许同时开发和细化相互连接的场景图和常识图的丰富的、异构的结构。

Knowledge graphs

将知识图谱定义为实体和谓词节点的集合，每个节点都有一个语义标签，以及一组来自预定义类型集的有向加权边。定义一个节点类型 ∆ ，则编码 ∆ 和 ∆^{\prime} 类型节点之间关系r的边集定义为：

\mathcal{E}_{r}^{\Delta \rightarrow \Delta^{\prime}} \subseteq \mathcal{N}_{\Delta} \times \mathcal{N}_{\Delta^{\prime}} \rightarrow \mathbb{R}

commonsense graph

常识图的每个节点表示其语义标签的一般概念，因此每个语义标签恰好出现在一个节点中。在这样一个图中，每条边编码一个涉及一对概念的关系事实，例如Hand-partOf-Person和Cup-usedFor-Drinking。在形式上，将常识性实体节点 N_{CE} 和常识性谓词节点 N_{CP} 的集合定义为任务中的所有实体和谓词类。根据源节点和目标节点的类型，常识边 \mathcal{E}_C 由4个不同的子集组成:

\begin{aligned} \mathcal{E}_{\mathrm{C}}=&\left\{\mathcal{E}_{r}^{\mathrm{CE} \rightarrow \mathrm{CP}}\right\} \cup\left\{\mathcal{E}_{r}^{\mathrm{CP} \rightarrow \mathrm{CE}}\right\} \cup \\ &\left\{\mathcal{E}_{r}^{\mathrm{CE} \rightarrow \mathrm{CE}}\right\} \cup\left\{\mathcal{E}_{r}^{\mathrm{CP} \rightarrow \mathrm{CP}}\right\} \end{aligned}

scene graph

每个场景实体(SE)节点与一个边界框相关，每个场景谓词(SP)节点与一个有序对SE节点(主语与宾语)有关，有两种类型的无向边连接每个SP分别对应的主语和宾语。在这里，因为将知识边定义为有向的，所以本文将每个无向的主语或宾语的边建模为两个方向相反的有向边，每条边都有不同的类型

\begin{aligned} \mathcal{N}_{\mathrm{SE}} &\subseteq[0,1]^{4} \times \mathcal{N}_{\mathrm{CE}} \\ \mathcal{N}_{\mathrm{SP}} &\subseteq \mathcal{N}_{\mathrm{SE}} \times \mathcal{N}_{\mathrm{SE}} \times \mathcal{N}_{\mathrm{CP}} \\ \mathcal{E}_{\mathrm{S}}=&\left\{\mathcal{E}_{\text {subjectof }}^{\mathrm{SE} \rightarrow \mathrm{SP}}, \mathcal{E}_{\text {objectof }}^{\mathrm{SE} \rightarrow \mathrm{SP}},\right.\\ & \mathcal{E}_{\text {hasSubject }}^{\mathrm{SP} \rightarrow \mathrm{SE}}, \mathcal{E}_{\text {hasobject }}^{\mathrm{SP} \rightarrow \mathrm{SE}}\} \end{aligned}

其中 [0,1]^4 为可能的边界框的集合， \mathcal{N}_{SE}×\mathcal{N}_{SE}×\mathcal{N}_{CP} 为由两个场景实体节点和一个场景谓词节点组成的所有可能的三元组的集合。

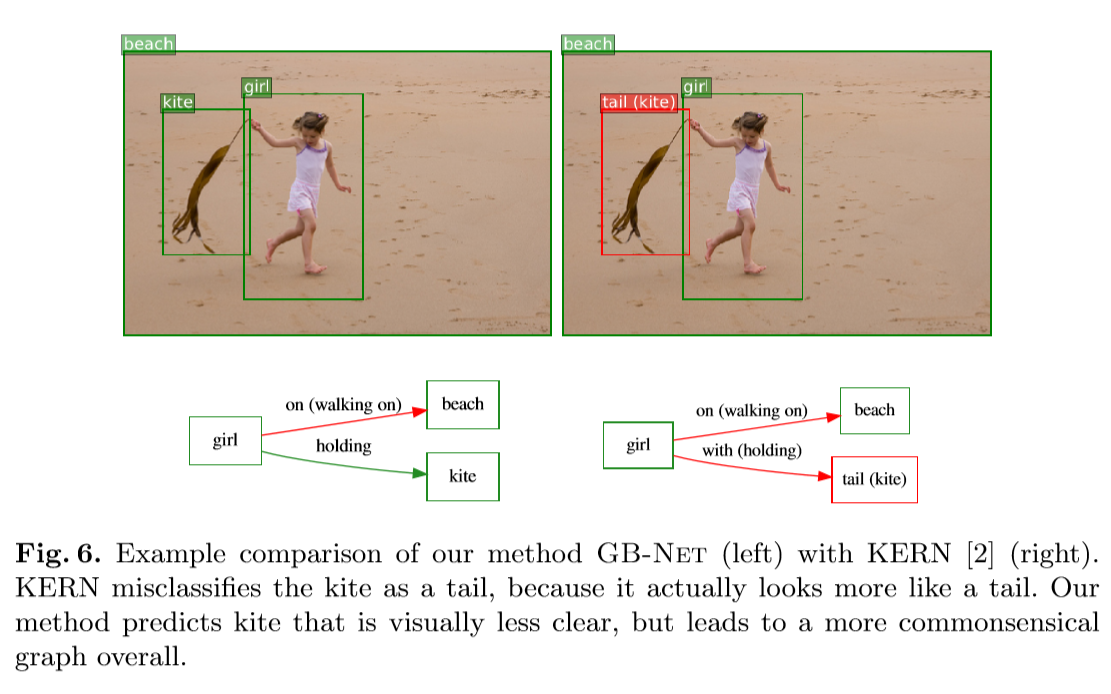
上图显示了场景图和常识图的示例，以便更清楚地显示它们的相似性。这里假设每个场景图节点都有一个存在于常识图中的标签，因为在现实中一些对象和谓词可能属于背景类，所以将一个特殊的常识图节点视为背景实体，另一个作为背景谓词。

Bridging knowledge graphs

考虑到常识图公式与场景图公式的相似性，本文对公式进行了细微的改进，以实现这两种图之间的连接。具体来说，将类从SE和SP节点中移除，而将其编码为一组连接边 \mathcal{E}_B ，连接每个SE或SP节点与其对应的类，即对于一个CE或一个CP节点：

\begin{aligned} \mathcal{N}_{\mathrm{SE}}^{?} &\subseteq[0,1]^{4} \\ \mathcal{N}_{\mathrm{SP}}^{?} &\subseteq \mathcal{N}_{\mathrm{SE}} \times \mathcal{N}_{\mathrm{SE}} \\ \mathcal{E}_{\mathrm{B}}=&\left\{\mathcal{E}_{\text {classifiedTo }}^{\mathrm{SE} \rightarrow \mathrm{CE}}, \mathcal{E}_{\text {classifiedTo }}^{\mathrm{SP} \rightarrow \mathrm{CP}},\right.\\ & \mathcal{E}_{\text {hasInstance }}^{\mathrm{CE} \rightarrow \mathrm{SE}}, \mathcal{E}_{\text {hasInstance }}^{\mathrm{CP} \rightarrow \mathrm{SP}}\} \end{aligned}

其中 .^? 表示节点是隐式的，即它们的类是未知的。类型为classifiedTo的边，将一个实体或谓词连接到常识图中对应的标签，并有一条hasInstance类型的反向边，将常识节点连接回实例。在此基础上，可以将场景图生成的问题定义为从图像中提取隐含实体和谓词节点(称为scene graph proposal)，然后通过将每个实体或谓词连接到常识图中对应的节点对其进行分类。因此，给定输入图像I和提供的固定的常识图，具有常识知识的场景图生成的目标是最大化如下函数：

\begin{array}{c} p\left(\mathcal{N}_{\mathrm{SE}}, \mathcal{N}_{\mathrm{SP}}, \mathcal{E}_{\mathrm{S}} \mid I, \mathcal{N}_{\mathrm{CE}}, \mathcal{N}_{\mathrm{CP}}, \mathcal{E}_{\mathrm{C}}\right)= \\ p\left(\mathcal{N}_{\mathrm{SE}}^{?}, \mathcal{N}_{\mathrm{SP}}^{?}, \mathcal{E}_{\mathrm{S}} \mid I\right) \times \\ p\left(\mathcal{E}_{\mathrm{B}} \mid I, \mathcal{N}_{\mathrm{CE}}, \mathcal{N}_{\mathrm{CP}}, \mathcal{E}_{\mathrm{C}}, \mathcal{N}_{\mathrm{SE}}^{?}, \mathcal{N}_{\mathrm{SP}}^{?}, \mathcal{E}_{\mathrm{S}}\right) \end{array}

第一项是输入一个图像，经过区域候选网络推断出 \mathcal{N}_{\mathrm{SE}}^{?} ，然后是经过一个考虑所有可能实体对的简单的谓词建议算法得到 \mathcal{N}_{\mathrm{SP}}^{?} ；第二项是由本文提出的GB-NET来实现的(通过场景结构和常识图来推导连接边)。

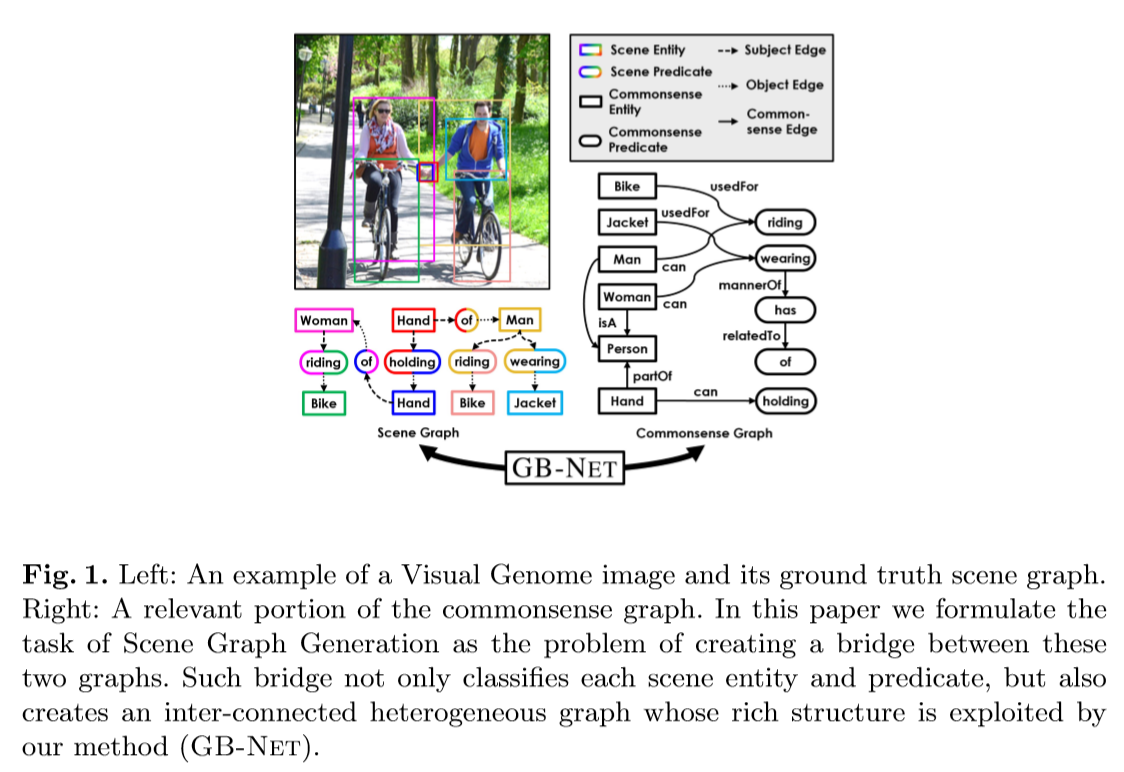
本文的方法

如上图所示，给定一幅图像，首先应用Faster R-CNN来检测物体，并将它们表示为场景实体(SE)节点。它还为每个实体创建一个场景谓词(SP)节点，形成一个有待分类的场景图候选。给定这个图和一个背景常识图，这两个图的内部连接固定，本文的目标是在这两个图之间创建连接每个实例(SE和SP节点)与其对应的类(CE和CP节点)的连接边。

为此，本文的模型通过连接SE与Faster R-CNN预测的标签相匹配的CE来初始化实体连接，并通过消息传播网络来更新节点表示，并使用它们来计算每个SP节点和CP节点的成对相似度，找到最大相似对并通过谓语连接去连接场景谓词和它对应的类，对于实体节点也执行相同的操作来优化实体连接，不断重复这两个过程，最后的连接将决定每个节点的类，从而产生输出场景图

Graph initialization

对象检测器输出n个检测对象的集合，每个检测对象有一个边界框 b_j ，一个标签分布 p_j 和一个RoI-aligned特征向量 v_j ，然后为每个对象分配一个场景实体节点(SE)，为每对对象分配一个场景谓词节点(SP)，以两个实体作为主语和宾语表示潜在谓词。

每个实体使用其RoI特征 v_j 进行初始化，每个谓词使用包围其主语和宾语的联合体的边界框的RoI特征 u_j 进行初始化

\mathbf{x}_{j}^{\mathrm{SE}}=\phi_{\text {init }}^{\mathrm{SE}}\left(\mathbf{v}_{j}\right), \quad \text { and } \quad \mathbf{x}_{j}^{\mathrm{SP}}=\phi_{\text {init }}^{\mathrm{SP}}\left(\mathbf{u}_{j}\right)

\phi_{\text {init }}^{\mathrm{SE}} 和 \phi_{\text {init }}^{\mathrm{SP}} 是ROI-align之后的两个全连接网络，为了得到场景图候选，本文通过有标签的边将每个谓词节点连接到它的主语和宾语，具体而言定义了四种边类型：对于一个三元组s-p-o，p->s使用hasSubject，p->o使用hasObject，s->p使用SubjectOf，o->p使用objectOf，将两个方向作为独立类型的原因是，在消息传递阶段，使用谓词信息更新实体的方式应该与使用实体更新谓词的方式不同。

另一方面，使用常识性实体节点(CE)和常识性谓词节点(CP)的单词嵌入的线性投影来初始化常识图：

\mathbf{x}_{i}^{\mathrm{CE}}=\phi_{\text {init }}^{\mathrm{CE}}\left(\mathbf{e}_{i}^{n}\right), \quad \text { and } \quad \mathbf{x}_{i}^{\mathrm{CP}}=\phi_{\text {init }}^{\mathrm{CP}}\left(\mathbf{e}_{i}^{p}\right)

由此得到两个独立的图：场景图和常识图，表示被检测到的Person的SE节点指的是实体中的人概念，即常识图中的Person节点，因此可以通过一个类别为classifiedTo的边去连接SE节点和Faster R-CNN预测的标签相匹配的CE节点，每个实体与前 K_{bridge} 个类别之间以 p_j (Faster R-CNN预测的类别的分布)的权重相连，同时还使用一个类别为hasInstance的边区连接CE节点与相应的SE节点，权重也为 p_j ，这是为了确保信息从常识流向场景，以及从场景流向常识，但方式不同。

同样为谓词定义了两种边的类型，classifiedTo和hasInstance，谓词最初是一个空集，将在连接SP节点和CP节点的时候更新，这四种类型的边可以被看作是连接两个固定图的桥梁，即本文模型所需要确定的隐变量。这就形成了一个具有四种类型节点(SE, SP, CE和CP)和各种类型边的异构图：如subjectOf类型的场景图边 \mathcal{E}_{\mathrm{S}} ，usedFor类型的常识边 \mathcal{E}_{\mathrm{C}} 和classifiedTo类型的桥边 \mathcal{E}_{\mathrm{B}} 。

Successive message passing and bridging

解释如何更新节点表示和桥边，同时保持常识图和场景图的边不变，本文使用GGNN的变体去进行节点信息的传播。

首先将节点表示传入一个全连接网络去计算传出消息：

\mathbf{m}_{i}^{\Delta \rightarrow}=\phi_{\text {send }}^{\Delta}(\mathbf{x}_{i}^{\Delta})

对于每个节点 i 和节点类型 ∆ ， \phi_{\text {send }} 是一个对所有类型节点权值共享的可训练的send head，在计算出传出消息之后，通过所有传出的边将它们发送出去，并乘以边的权值。

而对于每个节点，通过对聚合的消息应用另一个完全连接的网络来计算每个节点的传入消息，首先是相同类型的边之间，然后连接不同类型的边：

\mathbf{m}_{j}^{\Delta \leftarrow}=\phi_{\text {receive }} ^{\Delta}\left(\bigcup_{\Delta^{\prime}}\bigcup_{}^{\mathcal{E}_{k} \in \mathcal{E}^{\Delta^{\prime} \rightarrow \Delta}} \sum_{\left(i, j, a_{i j}^{k}\right) \in \mathcal{E}_{k}} a_{i j}^{k} \mathbf{m}_{i}^{\Delta^{\prime} \rightarrow}\right)

其中 \phi_{\text {receive}} 是一个可训练的receive head， \bigcup_{} 代表concat，第一个concat代表4种节点类型，第二个concat则代表所有的从类别 ∆^{\prime} 到类别 ∆ 的边，即聚合所有与j相连的边的信息，再通过GRU更新规则更新节点表示：

\begin{array}{l} \mathbf{z}_{j}^{\Delta}=\sigma\left(W_{z}^{\Delta} \mathbf{m}_{j}^{\Delta \leftarrow}+U_{z}^{\Delta} \mathbf{x}_{j}^{\Delta}\right) \\ \mathbf{r}_{j}^{\Delta}=\sigma\left(W_{r}^{\Delta} \mathbf{m}_{j}^{\Delta \leftarrow}+U_{r}^{\Delta} \mathbf{x}_{j}^{\Delta}\right) \\ \mathbf{h}_{j}^{\Delta}=\tanh \left(W_{h}^{\Delta} \mathbf{m}_{j}^{\Delta \leftarrow}+U_{h}^{\Delta}\left(\mathbf{r}_{j}^{\Delta} \odot \mathbf{x}_{j}^{\Delta}\right)\right), \\ \mathbf{x}_{j}^{\Delta} \Leftarrow\left(1-\mathbf{z}_{j}^{\Delta}\right) \odot \mathbf{x}_{j}^{\Delta}+\mathbf{z}_{j}^{\Delta} \odot \mathbf{h}_{j}^{\Delta} \end{array}

W^{\Delta} 和 U^{\Delta} 对不同节点类型不同，上式可以认为 \mathbf{x}_{j(t+1)}^{\Delta}=U(\mathbf{x}_{j(t)}^{\Delta}) ， U 是更新规则， t 代表时间步，上面部分为利用图的边更新节点表示，接下来介绍利用更新后的节点表示去更新桥梁的边 \mathcal{E}_{\mathrm{B}} ，即通过计算每个SE节点和所有CE节点以及每个SP节点和所有CP节点的配对相似度

\mathbf{a}_{i j}^{\mathrm{EB}}=\frac{\exp \left\langle\mathbf{x}_{i}^{\mathrm{SE}}, \mathbf{x}_{j}^{\mathrm{CE}}\right\rangle_{\mathrm{EB}}}{\sum_{j^{\prime}} \exp \left\langle\mathrm{x}_{i}^{\mathrm{SE}}, \mathbf{x}_{j^{\prime}}^{\mathrm{CE}}\right\rangle_{\mathrm{EB}}}, \quad \text { where } \quad\langle\mathbf{x}, \mathbf{y}\rangle_{\mathrm{EB}}=\phi_{\mathrm{att}}^{\mathrm{SE}}(\mathbf{x})^{T} \phi_{\mathrm{att}}^{\mathrm{CE}}(\mathbf{y}) \\ \mathbf{a}_{i j}^{\mathrm{PB}}=\frac{\exp \left\langle\mathbf{x}_{i}^{\mathrm{SP}}, \mathbf{x}_{j}^{\mathrm{CP}}\right\rangle_{\mathrm{PB}}}{\sum_{j^{\prime}} \exp \left\langle\mathrm{x}_{i}^{\mathrm{SP}}, \mathbf{x}_{j^{\prime}}^{\mathrm{CP}}\right\rangle_{\mathrm{PB}}}, \quad \text { where } \quad\langle\mathrm{x}, \mathbf{y}\rangle_{\mathrm{PB}}=\phi_{\mathrm{att}}^{\mathrm{SP}}(\mathrm{x})^{T} \phi_{\mathrm{att}}^{\mathrm{CP}}(\mathbf{y})

其中 \phi_{\mathrm{att}}^{\Delta} 是类似transformers的attention head的全连接网络，它对于不同的节点类型不同，故上式的相似度计算是不对称的， \mathbf{a}_{i j}^{\mathrm{EB}} 被表示为从 \mathbf{x}_{i}^{\mathrm{SE}} 到 \mathbf{x}_{j}^{\mathrm{CE}} 的classifiedTo边和从 \mathbf{x}_{j}^{\mathrm{CE}} 到 \mathbf{x}_{i}^{\mathrm{SE}} 的hasInstance边的权值，同理 \mathbf{a}_{i j}^{\mathrm{PB}} 被表示为 \mathbf{x}_{i}^{\mathrm{SP}} 和 \mathbf{x}_{j}^{\mathrm{CP}} 之间的边的权值

在初期实验时，意识到这种完全连接的桥会损害性能。因此只保留每个 i 的前 K_{bridge} 大的 \mathbf{a}_{i j}^{\mathrm{EB}} 值，并将其余值设置为零，对于谓词同理，通过重复上述两个步骤，最终的 \mathbf{a}_{i j}^{\mathrm{EB}} 和 \mathbf{a}_{i j}^{\mathrm{PB}} 是本文模型的输出,可以用来分类场景图中的每个实体和谓词。

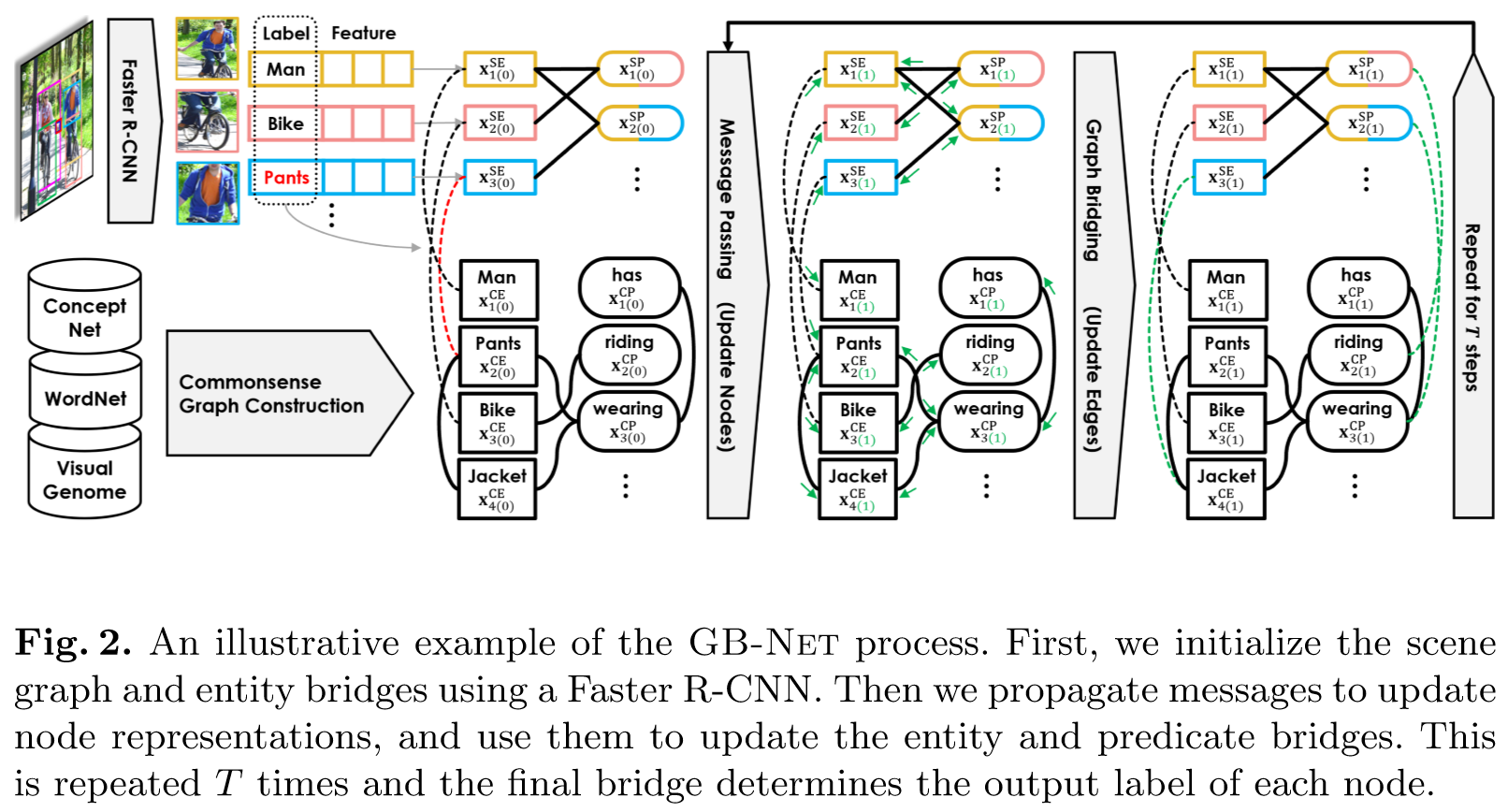
部分实验结果

相关文章